TP and TQ are any two tangents to a parabola and the tangent at a third point R cuts them in and , prove that .
1
2
3
none of these
The correct Answer is:A
Let parabola be and co-ordinates of P and Q on this parabola be and ,
T is the point of intersection of tangents at and . Co-ordinates of
Let
Similarly, .
Topper's Solved these Questions
- PARABOLABOOK - CENGAGE PUBLICATIONCHAPTER - PARABOLAEXERCISE - Multiple Correct Answers Type
10 Videos
- PARABOLABOOK - CENGAGE PUBLICATIONCHAPTER - PARABOLAEXERCISE - Matching Column Type
1 Videos
- PARABOLABOOK - CENGAGE PUBLICATIONCHAPTER - PARABOLAEXERCISE - Comprehension Type
2 Videos
- PAIR OF STRAIGHT LINESBOOK - CENGAGE PUBLICATIONCHAPTER - PAIR OF STRAIGHT LINESEXERCISE - Numberical Value Type
5 Videos
- PERMUTATION AND COMBINATIONBOOK - CENGAGE PUBLICATIONCHAPTER - PERMUTATION AND COMBINATIONEXERCISE - Comprehension
8 Videos
Similar Questions
Knowledge Check
TP and TQ are the tangents to a circle, with centre O. Find x.
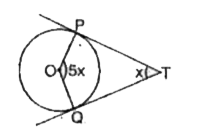 A15∘B60∘C30∘D45∘
A15∘B60∘C30∘D45∘If TP and TQ are two tangents to a circle with centre O, so that ∠POQ=120∘, then ∠PTQ is equal to
A120∘B30∘C60∘D90∘
If TPandTQ are the two tangents to a circle with centre O. so that ∠POQ=115∘, then ∠PTQ=……….(65∘).
View SolutionIf TP and TQ are the two tangents to a circle with centre O so that ∠POQ=110∘, then ∠PTQ is equal to
View SolutionTwo tangents TP and TQ are drawn to a circle with centre O from an external point T . Prove that ∠PTQ=2∠OPQ .
View SolutionTP&TQ are tangents to the parabola, y2=4ax at P and Q. If the chord passes through the point (−a,b) then the locus of T is
View SolutionTP and TQ are tangents to parabola y2=4x and normals at P and Q intersect at a point R on the curve. The locus of the centre of the circle circumseribing ΔTPQ is a parabola whose
View SolutionProve that the length of the tangent drawn from an external point to a circle are equal. Using the above, do the following: TP and TQ are tangents from T to the circle with circle O and R in any point on the circle. If AB is a tangent to the circle at R, prove that TA + AR =TB +BR.

View Solution
