Question

If the tangent at $(3,-4)$ to the circle $x^2+y^2-4x+2y-5=0$ cuts the circle $x^2+y^2+16x+2y+10=0$ in A and B then the midpoint of AB is

Answer

`(-6,-7)`

Explanation

Equation of tangent to circle `x^(2)+y^(2)-4x+2y-5=0` at point (3,-4) is
`3x-4y-2(x+3)=(y-4)-5=0`
or `x-3y-15=0` (1)

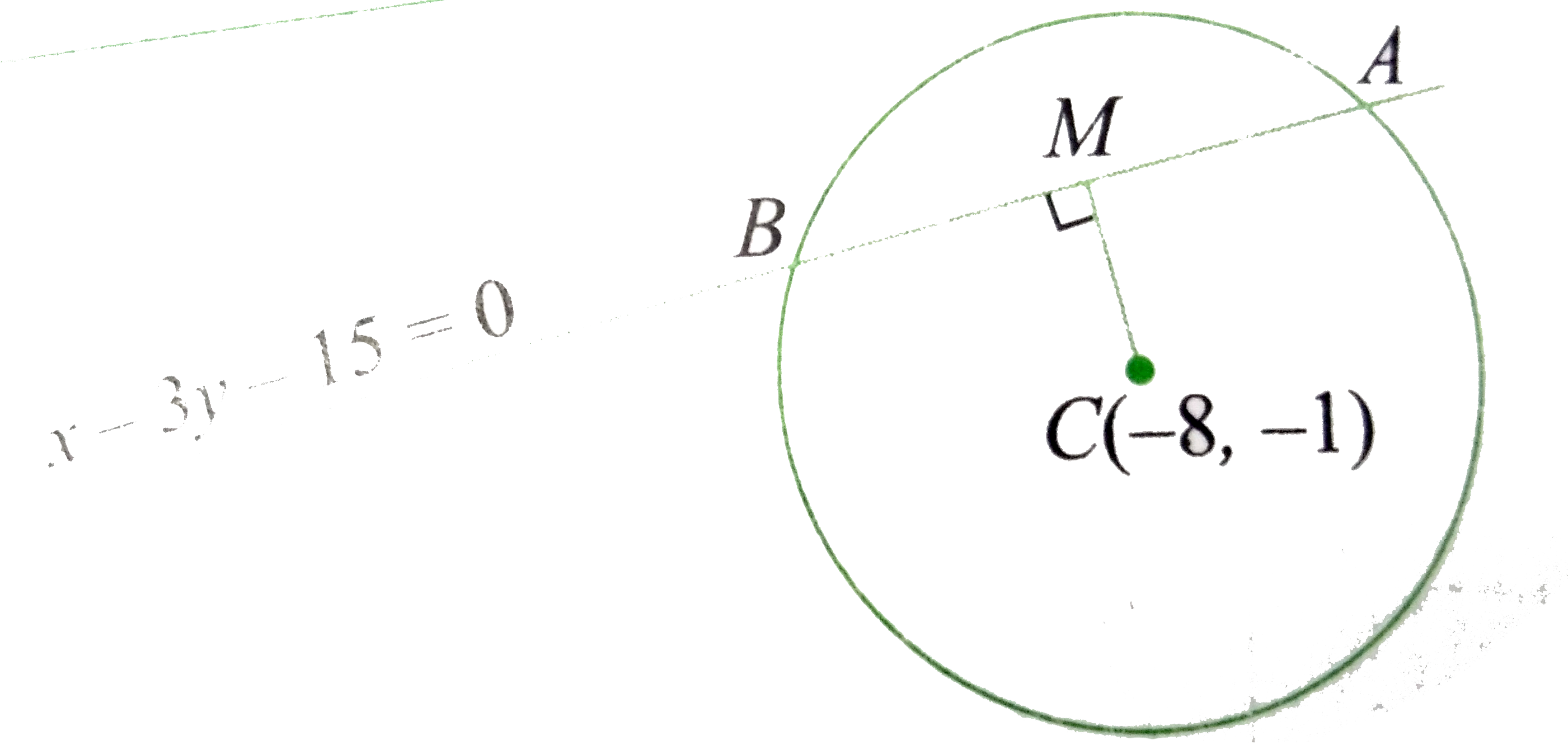
Center of the second circle is `C(-8,-1)`.
Slope of CM is `'-3'`
Equation of CM is `y+1= -3 (x+8)`
or `3x+y+25=0` (2)
Solving (1) and (2), we get `M -= (-6,-7)`