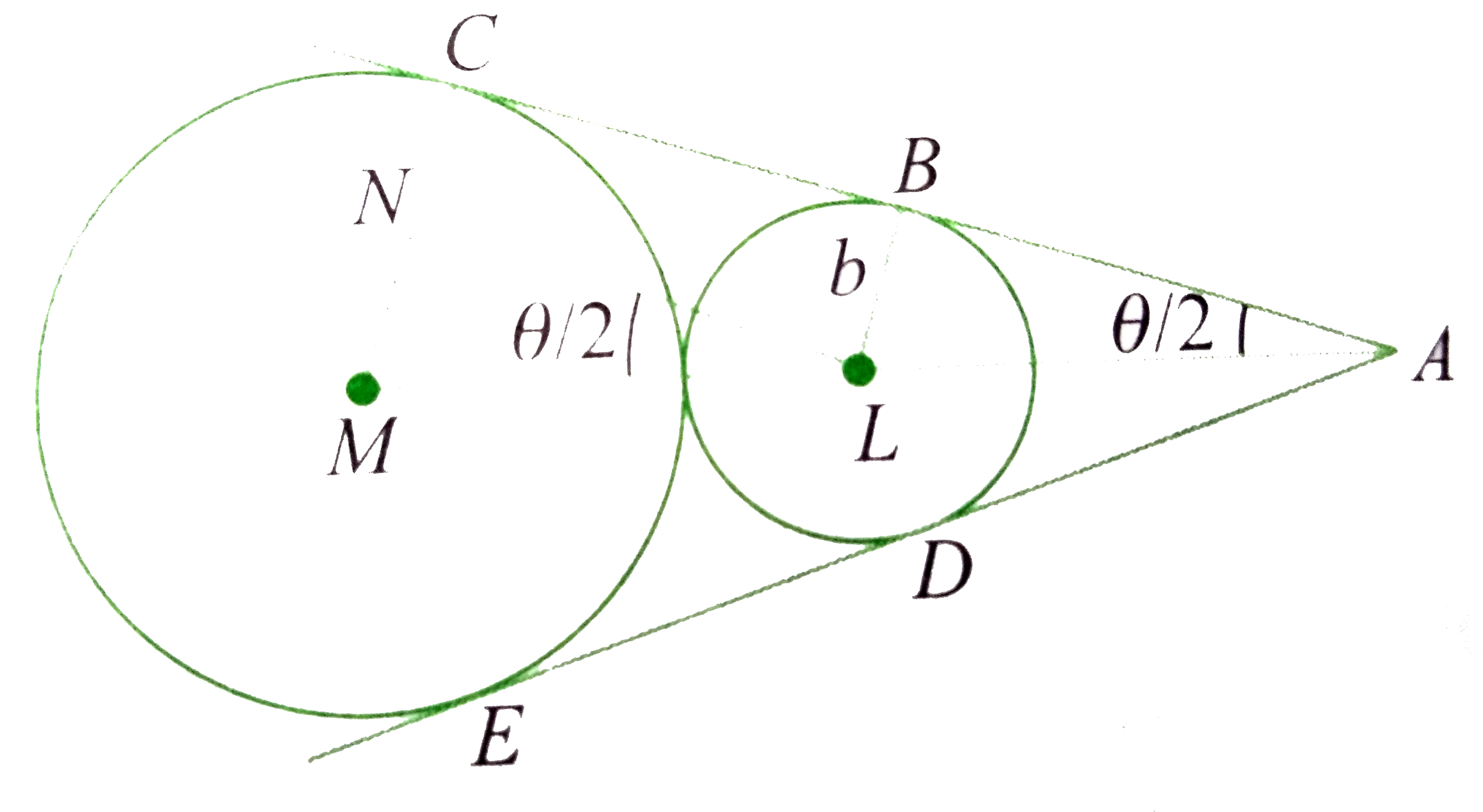
Two circles with radii aandb touch each other externally such that θ is the angle between the direct common tangents, (a>b≥2) . Then prove that θ=2sin−1(a−ba+b) .Solution in Bengali
From ΔMLN,
sin.θ2=a−ba+b
or θ2=sin−1(a−ba+b)
Therefore, the angle between AB and AD is
θ=2sin−1(a−ba+b)
Topper's Solved these Questions
- BOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLE EXERCISE - CONCEPT APPLICATION EXERCISE 4.181videos
CIRCLE
- BOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLE EXERCISE - CONCEPT APPLICATION EXERCISE 4.191videos
CIRCLE
- BOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLE EXERCISE - CONCEPT APPLICATION EXERCISE 4.134videos
CIRCLE
- BOOK - CENGAGE PUBLICATIONCHAPTER - BINOMIAL THEOREMEXERCISE - Comprehension11videos
BINOMIAL THEOREM
- BOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLESEXERCISE - Comprehension Type8videos
CIRCLES
Similar Questions
Find the middle point of the chord of the circle x2+y2=25 intercepted on the line x−2y=2
03:43View SolutionFind the locus of the midpoint of the chord of the circle x2+y2−2x−2y=0 , which makes an angle of 1200 at the center.
03:43View SolutionProve that the locus of the centroid of the triangle whose vertices are (acost,asint),(bsint,−bcost), and (1,0) , where t is a parameter, is circle.
02:26View SolutionConsider a G.P. with first term (1+x)n, |x|<1, common ratio 1+x2 and number of terms (n+1). Let 'S' be sum of all the terms of the G.P., then
The coefficient of xn is 'S' is03:52View Solution
In the diagram as shown, a circle is drawn with centre C(1,1) and radius 1 and a line L. The line L is tangent to the circle at Q. Further L meets the y-axis at R and the x-axis at P in such a way that the angle OPQ equals θ where 0<θ<π2.
Coordinate of Q is05:26View SolutionTwo circles with radii a and b touch each other externally such that theta is the angle between their direct common tangent (a>b>=2), then
07:32View SolutionTwo circles of radii a and b touch each other externally and theta be the angle between their direct common tangents (a>b>=2) then
02:12View SolutionTwo circles with radii aandb touch each other externally such that θ is the angle between the direct common tangents, (a>b≥2) . Then prove that θ=2sin−1(a−ba+b) .
05:46View SolutionTwo circles of radii 4cm and 1cm touch each other externally and θ is the angle contained by their direct common tangents. Then sinθ is equal to 2425 (b) 1225 34 (d) none of these
04:31View SolutionTwo circles of radii r1 and r2,r1>r2≥2 touch each other externally. If θ be the angle between the direct common tangents, then,
04:01View SolutionTwo circles with radii a and b respectively touch each other externally . Let c be the radius of a circle that touches these two circles as well as a common tangent to the circles. Then
02:58View SolutionTwo circles with radii a and b intersect each other externally in such a way that the angle between common tangents theta If so (a gt b ge 2)
04:53View SolutionTwo circles of radii 4cm and 1cm touch each other externally and θ is the angle contained by their direct common tangents. Find sin(θ2)+cos(θ2).
03:33View SolutionTwo circles with radii aandb touch each other externally such that θ is the angle between the direct common tangents, (a>b≥2) . Then prove that θ=2sin−1(a−ba+b) .
03:27View SolutionTwo circles with radii aandb touch each other externally such that θ is the angle between the direct common tangents, (a>b≥2) . Then prove that θ=2sin−1(a−ba+b) .
04:22View SolutionTwo circles of radii 4cm and 1cm touch each other externally and θ is the angle contained by their direct common tangents. Then sinθ is equal to (a)2425 (b) 1225 (c)34 (d) none of these
06:35View Solution

