A variable chord of the circle x2+y2=4 is drawn from the point P(3,5) meeting the circle at the point A and B. A point Q is taken on the chord such that 2PQ=PA+PB . The locus of Q is x2+y2+3x+4y=0 x2+y2=36 x2+y2=16 x2+y2−3x−5y=0Solution in Bengali
x2+y2+3x+4y=0
x2+y2=36
x2+y2=16
x2+y2−3x−5y=0
The correct Answer is:4
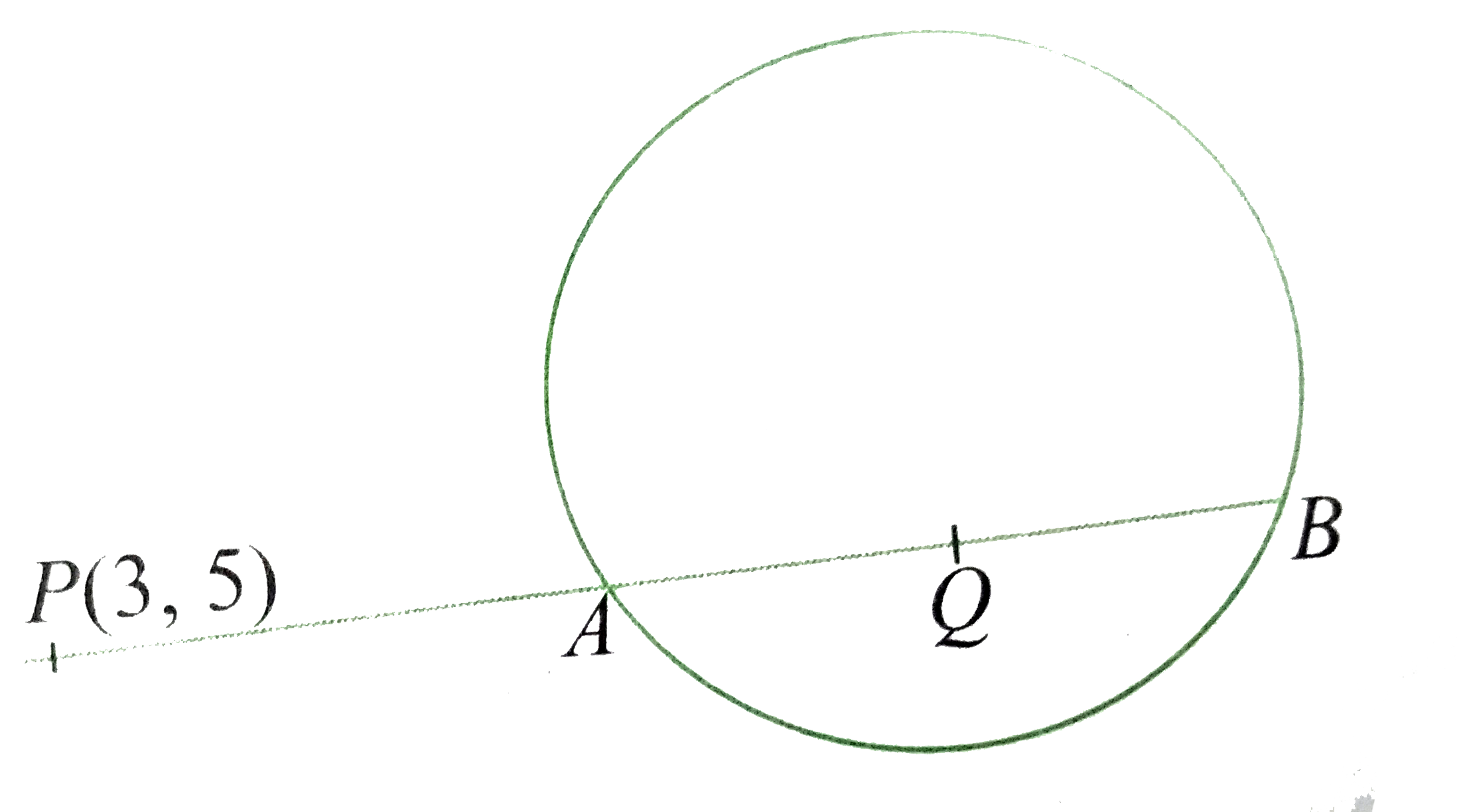
2PQ=PA+PB
or PQ−PA=PB−PQ
or AQ=QB
Therefore, Q is the midpoint of AB.
Let Q has coordinates (h,k).
Then the equation of chord AB is given by T=S1
or hx+ky−4=h2+k2−4
This variable chord passes through the point P(3,5). Therefore,
3h+5k=h2+k2
or x2+y2−3x−5y=0
which is the required locus.
Topper's Solved these Questions
- BOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLE EXERCISE - Multiple Correct Anser Type29videos
CIRCLE
- BOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLE EXERCISE - Linked Comprehension Type (For Problem 1-3)3videos
CIRCLE
- BOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLE EXERCISE - CONCEPT APPLICATION EXERCISE 4.172videos
CIRCLE
- BOOK - CENGAGE PUBLICATIONCHAPTER - BINOMIAL THEOREMEXERCISE - Comprehension11videos
BINOMIAL THEOREM
- BOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLESEXERCISE - Comprehension Type8videos
CIRCLES
Similar Questions
about to only mathematics
02:46View SolutionEach side of a square is of length 6 units and the centre of the square Is ( - 1, 2). One of its diagonals is parallel to x+y=0. Find the co-ordinates of the vertices of the square.
02:21View SolutionThree concentric circles of which the biggest is x2+y2=1, have their radii in A.P If the line y=x+1 cuts all the circles in real and distinct points. The interval in which the common difference of the A.P will lie is:
04:52View SolutionConsider a G.P. with first term (1+x)n, |x|<1, common ratio 1+x2 and number of terms (n+1). Let 'S' be sum of all the terms of the G.P., then
The coefficient of xn is 'S' is06:10View Solution
In the diagram as shown, a circle is drawn with centre C(1,1) and radius 1 and a line L. The line L is tangent to the circle at Q. Further L meets the y-axis at R and the x-axis at P in such a way that the angle OPQ equals θ where 0<θ<π2.
Coordinate of Q isView SolutionA variable chord of circle x^(2)+y^(2)=4 is drawn form the point P(3,5) meeting the circle at the point A and B. A point Q is taken on this chord such that 2PQ=PA+PB. Locus of point 'Q' is
View SolutionA variable chord of the circle x2+y2=4 is drawn from the point P(3,5) meeting the circle at the point A and B. A point Q is taken on the chord such that 2PQ=PA+PB . The locus of Q is x2+y2+3x+4y=0 x2+y2=36 x2+y2=16 x2+y2−3x−5y=0
03:07View SolutionA tangent at a point on the circle x2+y2=a2 intersects a concentric circle C at two points PandQ . The tangents to the circle X at PandQ meet at a point on the circle x2+y2=b2. Then the equation of the circle is x2+y2=ab x2+y2=(a−b)2 x2+y2=(a+b)2 x2+y2=a2+b2
03:39View SolutionA tangent is drawn at any point P(t) on the parabola y^(2)=8x and on it is taken a point Q(alpha,beta) from which pair of tangent QA and QB are drawn to the circle x^(2)+y^(2)=4. The locus of the point of concurrency of the chord of contact AB of the circle x^(2)+y^(2)=4 is
03:40View SolutionA line through the origin meets the circle x2+y2=a2 at P and the hyperbola x2−y2=a2 at. Q the locus of the point of intersection of the tangents at P to the circle and with the tangents at Q to the hyperbola is
03:40View SolutionIf the polar of a point on the circle x2+y2=p2 with respect to the circle x2+y2=q2 touches the circle x2+y2=r2 then p,q r are in
06:35View SolutionIf the chord of contact of the circle x2+y2=a2 with respect to a variable point P touches the parabola y2=4ax,then the equation of locus of P is
05:53View SolutionIf two distinct chords, drawn from the point (p, q) on the circle x^2+y^2=p x+q y (where p q!=q) are bisected by the x-axis, then p^2=q^2 (b) p^2=8q^2 p^2 8q^2
05:35View SolutionA variable chord of the circle x2+y2=4 is drawn from the point P(3,5) meeting the circle at the point A and B. A point Q is taken on the chord such that 2PQ=PA+PB . The locus of Q is x2+y2+3x+4y=0 x2+y2=36 x2+y2=16 x2+y2−3x−5y=0
05:06View SolutionIf P and Q are the points of intersection of the circles x^2+y^2+3x+7y+2p=0 and x^2+y^2+2x+2y-p^2=0 then there is a circle passing through P,Q and (1,1) for
03:44View SolutionA tangent is drawn at any point P(t) on the parabola y2=8x and on it is taken a point Q(α,β) from which pair of tangent QA and QB are drawn to the circle x2+y2=4. The locus of the point of concurrency of the chord of contact AB of the circle x2+y2=4 is
04:11View Solution

