Any circle through the point of intersection of the lines x+√3y=1 and √3x−y=2 intersects there lines at points PandQ . Then the angle subtended by the are PQ at its center is 1800 (b) 900 (c) 1200 depends on center and radiusSolution in Bengali
180∘
90∘
120∘
Depends on centre and radius
The correct Answer is:1
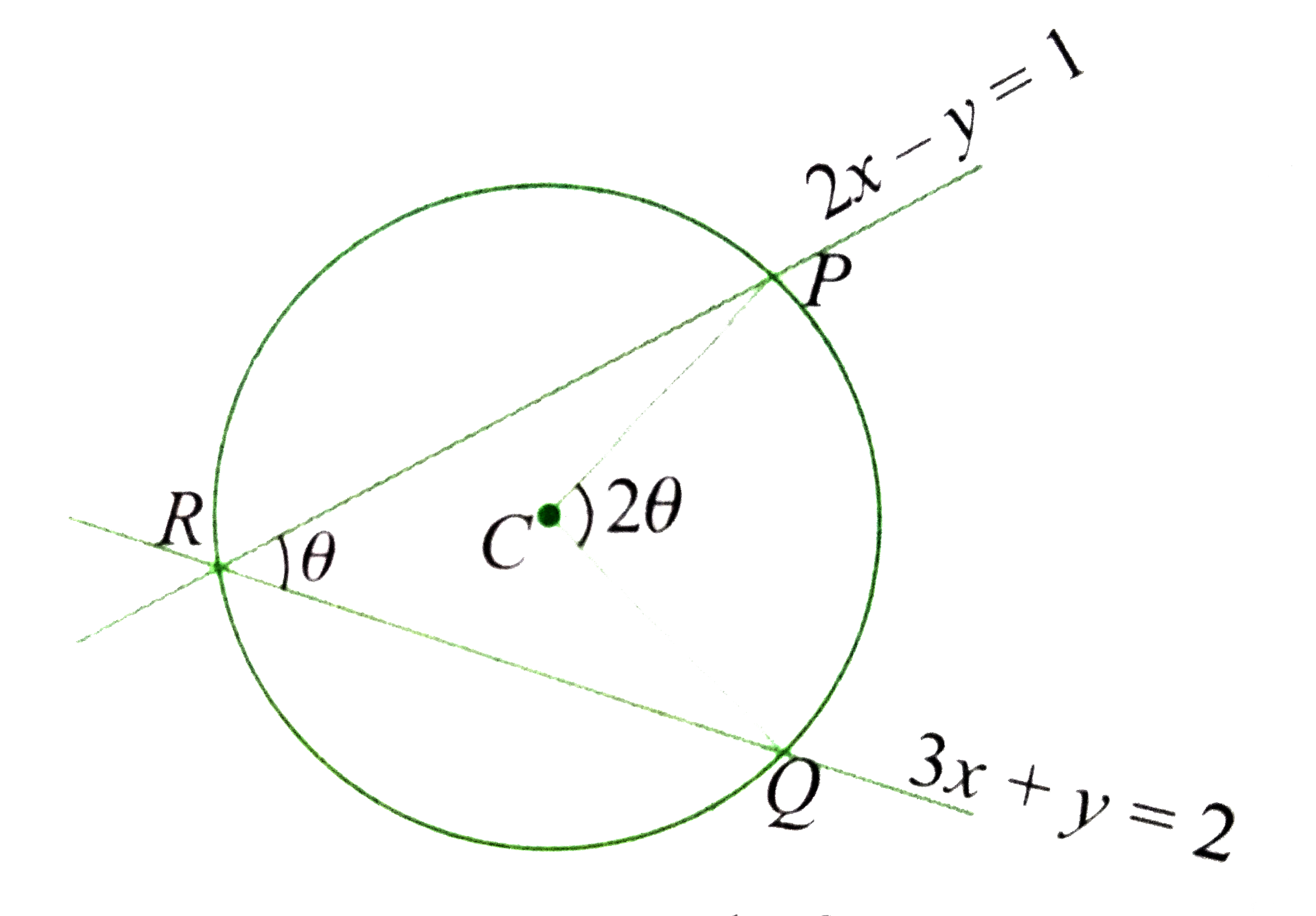
Slopes of gives lines are 2 and −3.
If angle between lines is θ , then
tanθ=∣∣∣2−(−3)1+(2)×(−3)∣∣∣=1
∴θ=∠PRQ=45∘
Topper's Solved these Questions
- BOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLE EXERCISE - Multiple Correct Anser Type29videos
CIRCLE
- BOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLE EXERCISE - Linked Comprehension Type (For Problem 1-3)3videos
CIRCLE
- BOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLE EXERCISE - CONCEPT APPLICATION EXERCISE 4.172videos
CIRCLE
- BOOK - CENGAGE PUBLICATIONCHAPTER - BINOMIAL THEOREMEXERCISE - Comprehension11videos
BINOMIAL THEOREM
- BOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLESEXERCISE - Comprehension Type8videos
CIRCLES
Similar Questions
about to only mathematics
06:38View SolutionEach side of a square is of length 6 units and the centre of the square Is ( - 1, 2). One of its diagonals is parallel to x+y=0. Find the co-ordinates of the vertices of the square.
02:16View SolutionThree concentric circles of which the biggest is x2+y2=1, have their radii in A.P If the line y=x+1 cuts all the circles in real and distinct points. The interval in which the common difference of the A.P will lie is:
02:45View SolutionConsider a G.P. with first term (1+x)n, |x|<1, common ratio 1+x2 and number of terms (n+1). Let 'S' be sum of all the terms of the G.P., then
The coefficient of xn is 'S' is03:56View Solution
In the diagram as shown, a circle is drawn with centre C(1,1) and radius 1 and a line L. The line L is tangent to the circle at Q. Further L meets the y-axis at R and the x-axis at P in such a way that the angle OPQ equals θ where 0<θ<π2.
Coordinate of Q is03:56View SolutionA straight line through the point (2,2) intersects the lines √3x+y=0 and √3x−y=0 at the point A and B, respectively. Then find the equation of the line AB so that triangle OAB is equilateral.
02:32View SolutionAny circle through the point of intersection of the lines x+√3y=1 and √3x−y=2 intersects these lines at points PandQ . Then the angle subtended by the arc PQ at its center is 1800 (b) 900 (c) 1200 depends on center and radius
04:25View SolutionA circle passes through the points of intersection of the line x=0 and the circle x^(2)+y^(2)+2x=3. If this circle passes through (sqrt(3),0) then its centre is :
01:49View Solutionरेखाओ x+3y=0 तथा 2x−7y=0 के प्रतिच्छेद बिंदु से जाने उस वृत्त का समीकरण ज्ञात कीजिए जिसका केंद्र रेखाओ x+y+1=0 तथा x−2y+4=0 का प्रतिच्छेद बिंदु है ।
04:56View Solutionx+3y=0 तथा 2x−7y=0 के कटान बिन्दु से जाते हुए वृत्त का समीकरण निकाले जिसका केन्द्र रेखाओं x+y+1=0 तथा x−2y+4=0 का प्रतिच्छेद बिन्दु है।
08:08View SolutionA straight line through the point (2, 2) intersects the lines √3x+y=0 and √3x−y=0 at the points A and B. The equation of the line AB so that ΔOAB is equilateral, is:
03:11View SolutionA straight line through the point (2, 2) intersects the lines √3x+y=0 and √3x−y=0 at the points A and B. The equation to the line AB so that the triangle OAB is equilateral is
02:08View SolutionA st. line through the point (2, 2) intersects the lines √3x+y=0and√3x−y=0 at the points A and B. The equation to the line AB so that the triangle OAB is equilateral is :
03:53View SolutionIf the circles x2+y2+2ax+cy+a=0 and x2+y2−3ax+dy−1=0 intersects at points P and Q , then find the values of a for which the line 5x+by−a=0 passes through PandQ.
10:43View SolutionAny circle through the point of intersection of the lines x+√3y=1 and √3x−y=2 intersects these lines at points PandQ . Then the angle subtended by the arc PQ at its center is 1800 (b) 900 (c) 1200 depends on center and radius
04:46View SolutionAny circle through the point of intersection of the lines x+√3y=1 and √3x−y=2 intersects there lines at points PandQ . Then the angle subtended by the are PQ at its center is 1800 (b) 900 (c) 1200 depends on center and radius
05:18View Solution

