Through the point P(3,4) a pair of perpendicular lines are drawn which meet x-axis at the point A and B. The locus of incentre of triangle PAB is (a) $x^{2} - y^{2} - 6 x - 8 y + 25 = 0$ (b) $x^{2} + y^{2} - 6 x - 8 y + 25 = 0$ (c) $x^{2} - y^{2} + 6 x + 8 y + 25 = 0$ (d) $x^{2} + y^{2} + 6 x + 8 y + 25 = 0$

A

$x^{2} - y^{2} - 6 x - 8 y + 25 = 0$

B

$x^{2} + y^{2} - 6 x - 8 y + 25 = 0$

C

$x^{2} - y^{2} + 6 x + 8 y + 25 = 0$

D

$x^{2} + y^{2} + 6 x + 8 y + 25 = 0$

Text Solution

Verified by Experts

The correct Answer is:1

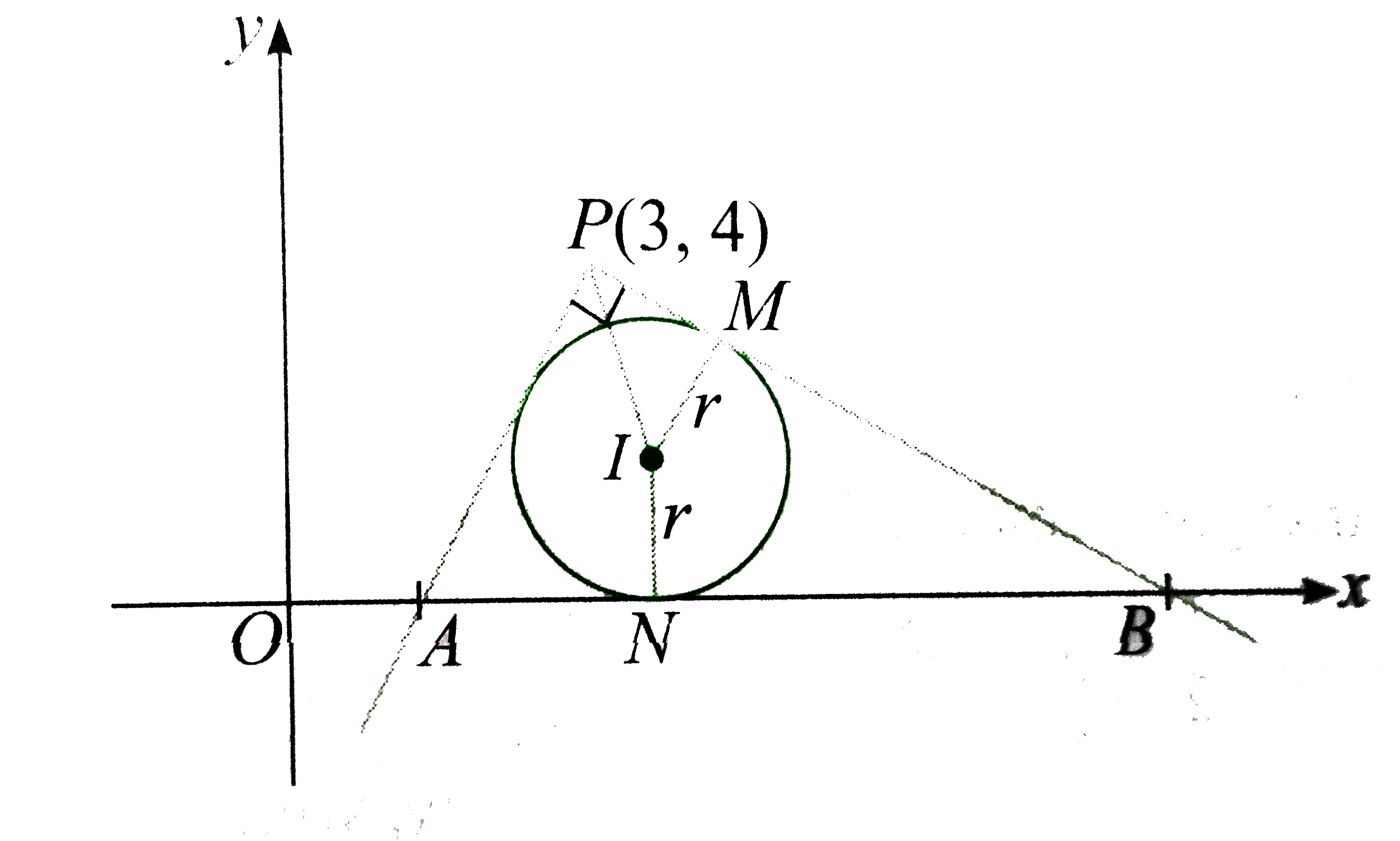
Let point I be (h,k).
From the figure,
$I P = r cos e c 45^{\circ},$ where $r =$ inradius
$\Rightarrow {(I P)}^{2} = 2 r^{2}$
$\Rightarrow {(3 - h)}^{2} + {(4 - k)}^{2} = 2 {(| k |)}^{2}$
( As circle touches x-axis, $r = {(| k |)}^{2}$
$\Rightarrow x^{2} - y^{2} - 6 x - 8 y + 25 = 0$ , which is the require locus.

|

Updated on:21/07/2023

Class 12 MATHS CIRCLE

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The circles $x^{2} + y^{2} - 6 x - 8 y = 0 and x^{2} + y^{2} - 6 x + 8 = 0$ are
Ainteresting in two points
Bnon-interesting
Ctouching externally
Dtouching internally
Question 2 - Select One
The circles $x^{2} + y^{2} - 6 x - 8 y = 0$ and $x^{2} + y^{2} - 6 x + 8 = 0$ are
Aintersecting in two points
Bnon-intersecting
Ctouching externally
Dtouching internally

CENGAGE PUBLICATION-CIRCLE -Excercises (Single Correct Answer Type)

Home
Ask Doubt
Profile