A light ray gets reflected from the x=-2. If the reflected ray touches the circle x2+y2=4 and point of incident is (-2,-4), then equation of incident ray is
4y+3x+22=0
3y+4x+20=0
4y+2x+20=0
y+x+6=0
The correct Answer is:1
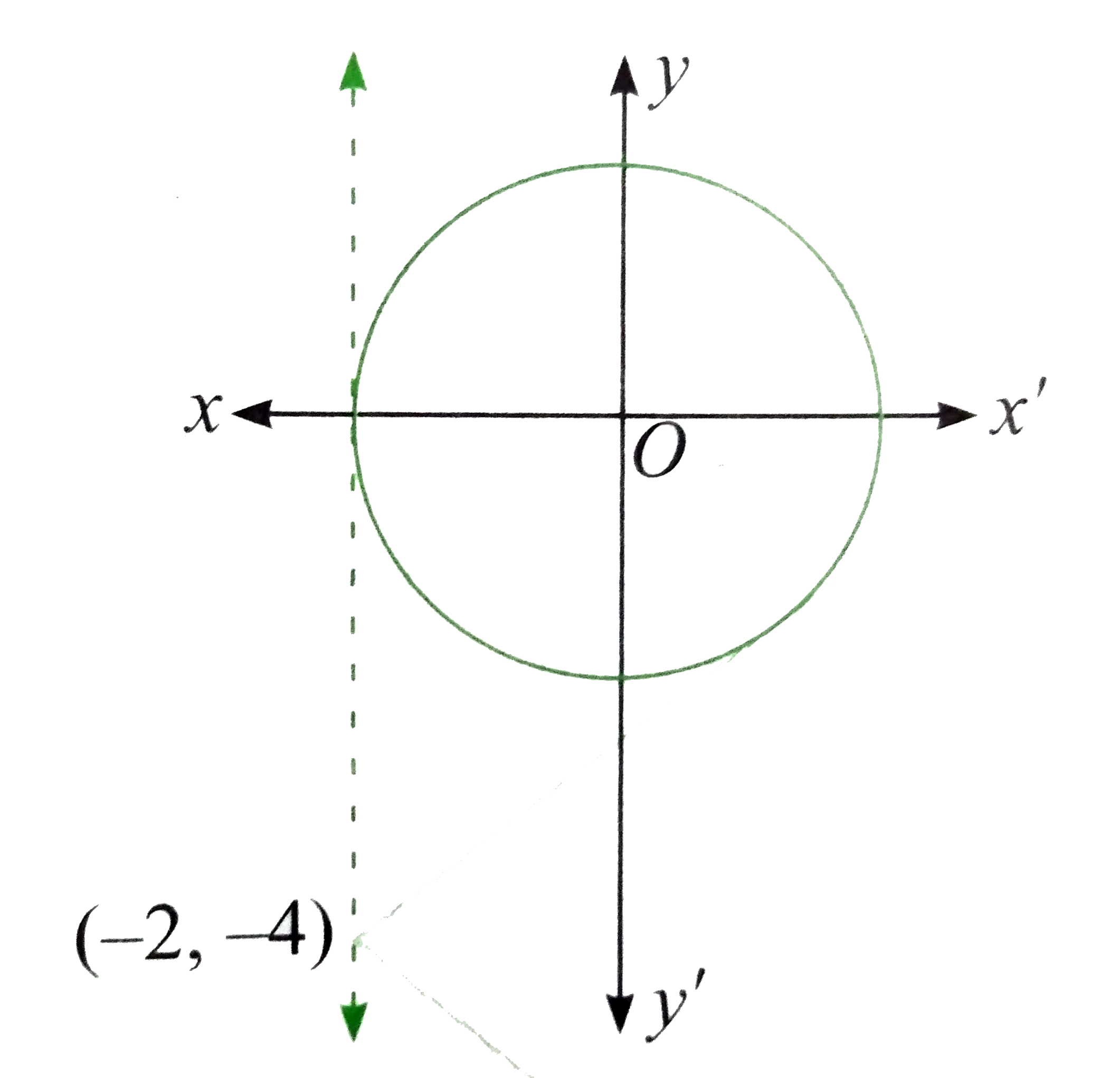
Any tangent of x2+y2=4 is y=mx±2√1+mk2. If it passes through (−2,−4), then
or 4m2−4)2=4(1+m2)
or 4m2+16−16m=4+4m2
or m=∞,m=34
Hence, the slope of the reflected ray is 3/4
Thus, the equation of the incident rays is
(y+4)=−34(x+2) i.e., 4y+3x+22=0
Topper's Solved these Questions
- CIRCLE BOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLE EXERCISE - Multiple Correct Anser Type
29 Videos
- CIRCLE BOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLE EXERCISE - Linked Comprehension Type (For Problem 1-3)
3 Videos
- CIRCLE BOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLE EXERCISE - CONCEPT APPLICATION EXERCISE 4.17
2 Videos
- BINOMIAL THEOREMBOOK - CENGAGE PUBLICATIONCHAPTER - BINOMIAL THEOREMEXERCISE - Comprehension
11 Videos
- CIRCLESBOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLESEXERCISE - Comprehension Type
8 Videos
Similar Questions
Statement I A ray of light incident at the point (-3,-1) gets reflected from the tangent at (0,-1) to the circle x2+y2=1. If the reflected ray touches the circle, then equation of the reflected ray is 4y-3x=5
Statement II The angle of incidence = angle of reflection i.e. ∠i=∠r,
View SolutionA ray of light incident at the point (-2, -1) gets reflected from the tangent at (0, -1) to the circle x2+y2=1. The reflected ray touches the circle. The equation of the line along which the incident ray moved is
View Solution
Knowledge Check
A light ray gets reflected by y-axis. If the point of incidence is (0,-2) and reflected ray touches the circle x2+y2−2x−2y+1=0, then the equationof incident ray is
A4x−3y−6=0B4x+3y+6=0Cx−y−2=0Dx+y+2=0Statement I A ray of light incident at the point (-3,-1) gets reflected from the tangent at (0,-1) to the circle x2+y2=1. If the reflected ray touches the circle, then equation of the reflected ray is 4y-3x=5
Statement II The angle of incidence = angle of reflection i.e. ∠i=∠r,AStatement I is true, Statement II is true, Statement II is a correct explanation for Statement IBStatement I is true, Statement II is true, Statement II is not a correct explanation for Statement ICStatement I is true, Statement II is falseDStatement I is false, Statement II is trueA light ray is incident on a smooth reflecting surface making an angle of incidence 2i. If the angle of incidence is doubled, then the deviation of the light ray is equal to ______ .
A90-40iB90-2iC2iD180-8i
A ray of light incident at the point (-2, -1) gets reflected from the tangent at (0, -1) to the circle x2+y2=1. The reflected ray touches the circle. The equation of the line along which the incident ray moved is
View SolutionA light ray gets reflected from a pair of mutually ⊥ mirrors, not necessarily along axes. The intersection point of mirrors is at origin. The incident light ray is along y=x+2 . If the light ray strikes both mirrors in succession, then it may get reflected finally along the line:
View SolutionAn incident ray is coming along the straight line y=4 and it strikes the parabola y2=4x, then equation of the reflected ray is
View SolutionThe diagram below shows a light ray striking and reflecting from a plane mirror AO is the incident ray and OB the reflected ray. The angle between the incident ray and the reflected ray is 120∘.
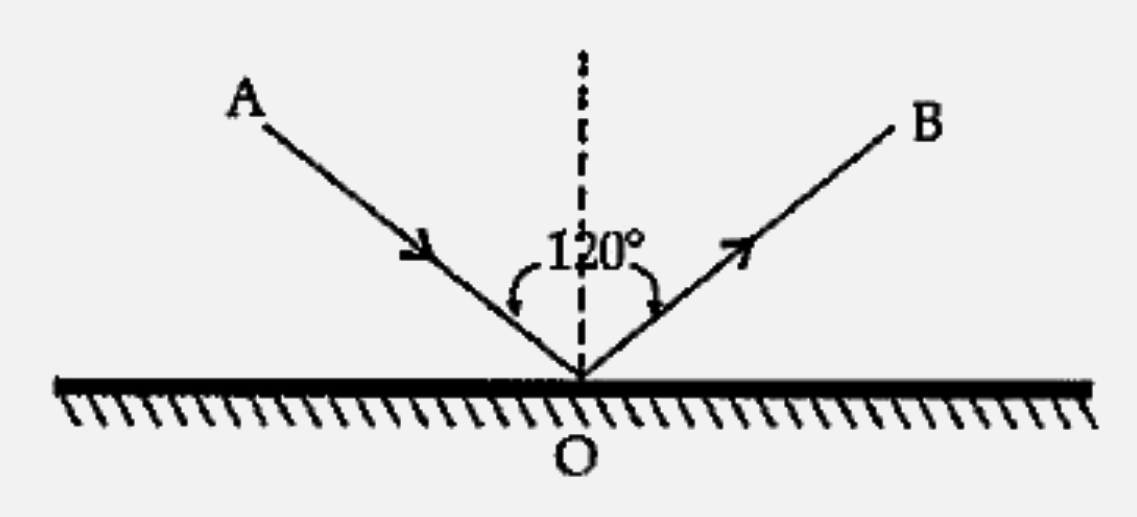
What is the value of the angle of reflection?
View SolutionA light ray is incident on a smooth reflecting surface making an angle of incidence 2i. If the angle of incidence is doubled, then the deviation of the light ray is equal to ______ .
View Solution
