Match the conics in List I with the statements/expressions in List II


Text Solution
The correct Answer is:r→p
|0+0−1|√h2+k2=2
⇒1=4(k2+h2)
∴h2+k2=(12)2 which is a circle.
Note : Solutions of the remaining parts are given in their repective chapters.
|
Topper's Solved these Questions
- CIRCLE BOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLE EXERCISE - NUMERICAL VALUE TYPE
21 Videos
- CIRCLE BOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLE EXERCISE - ARCHIVES (JEE MAIN)
1 Videos
- CIRCLE BOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLE EXERCISE - For Problems
43 Videos
- BINOMIAL THEOREMBOOK - CENGAGE PUBLICATIONCHAPTER - BINOMIAL THEOREMEXERCISE - Comprehension
11 Videos
- CIRCLESBOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLESEXERCISE - Comprehension Type
8 Videos
Similar Questions
Knowledge Check
Match the List-I and List-II:
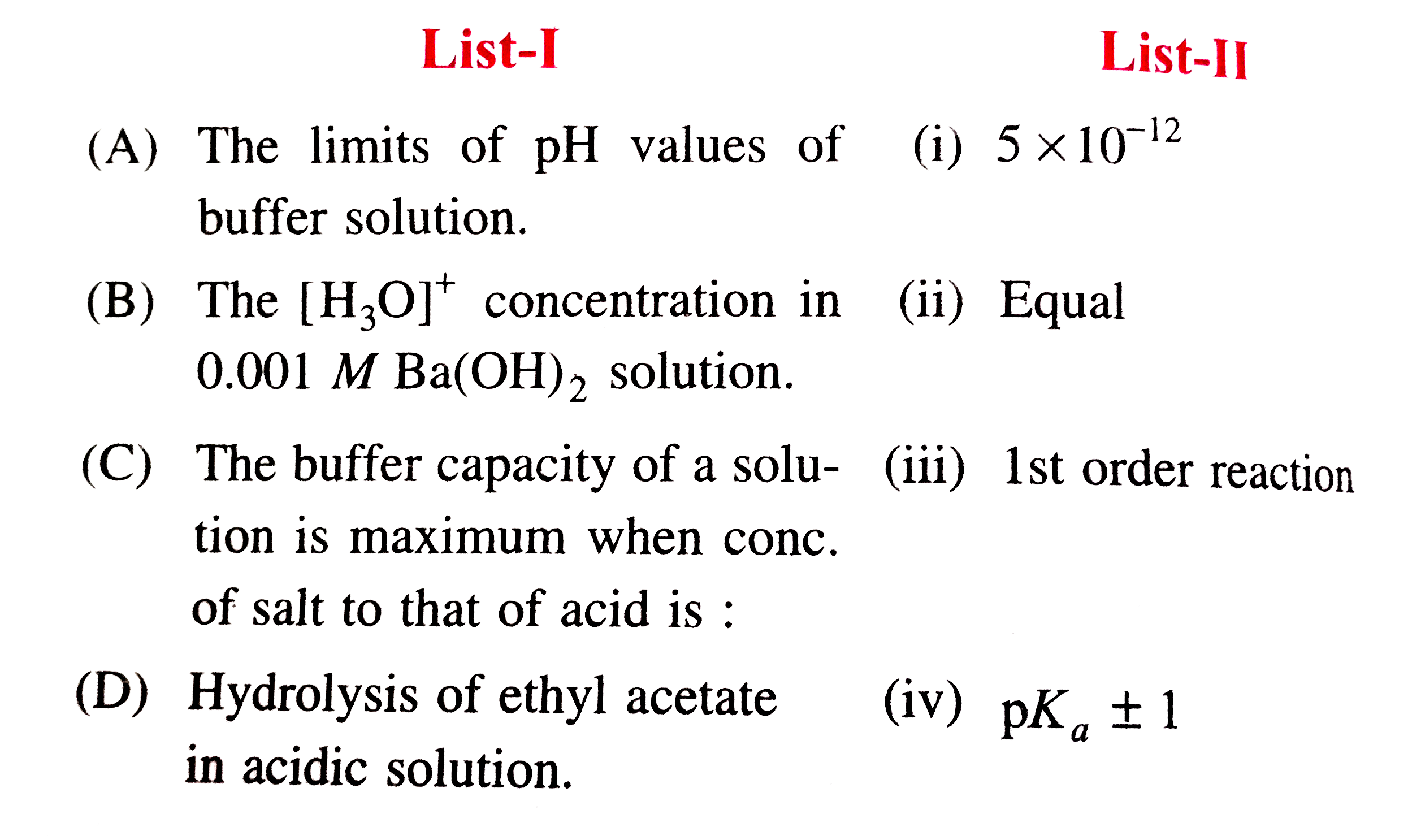 A(A)(B)(C)(D)iviiiiiiB(A)(B)(C)(D)iviiiiiiC(A)(B)(C)(D)iiviiiiiD(A)(B)(C)(D)iviiiiii
A(A)(B)(C)(D)iviiiiiiB(A)(B)(C)(D)iviiiiiiC(A)(B)(C)(D)iiviiiiiD(A)(B)(C)(D)iviiiiiiMatch the List-I and List-II:
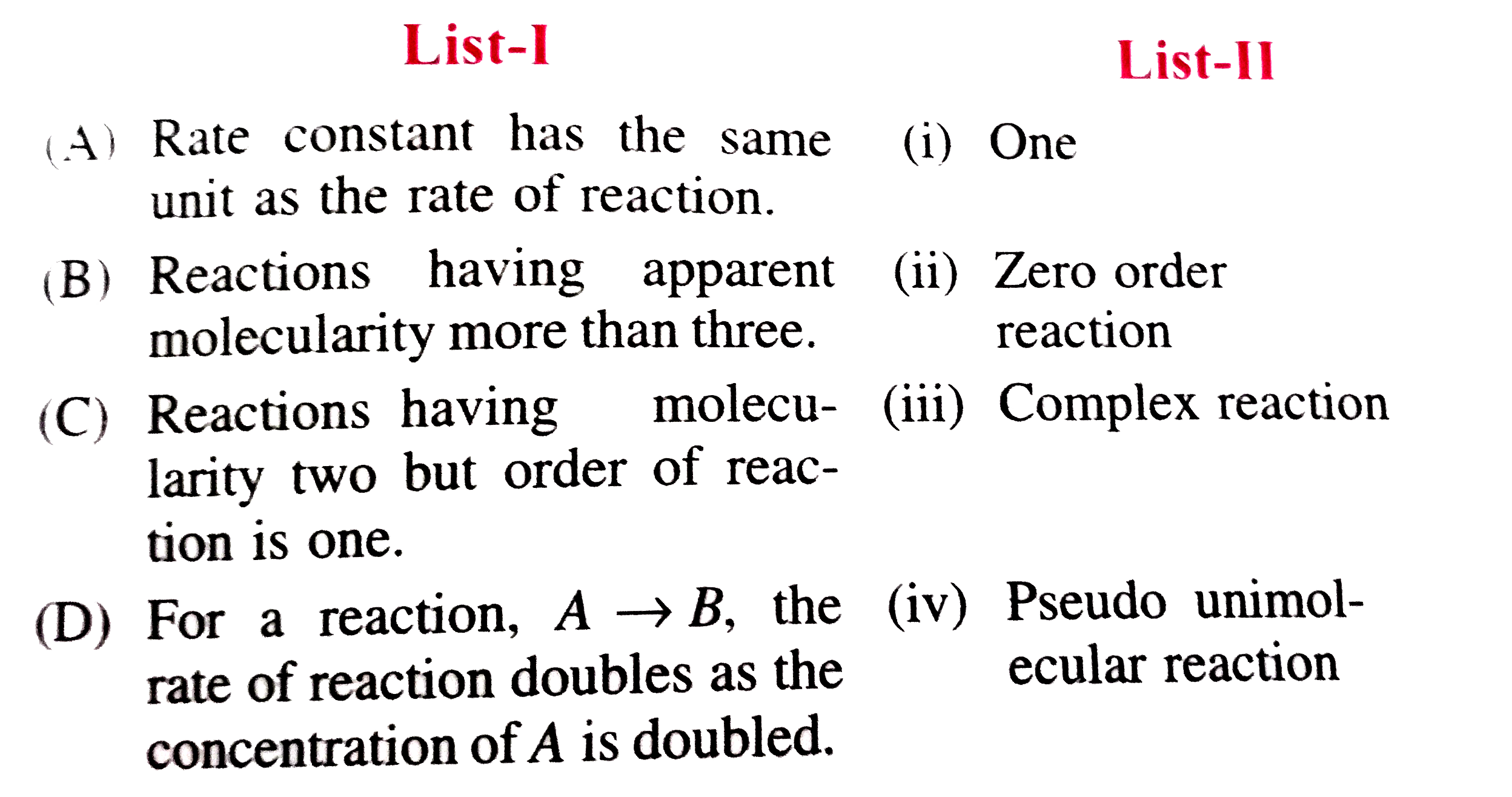 A(A)(B)(C)(D)iiiviiiiB(A)(B)(C)(D)iiiiiiviC(A)(B)(C)(D)iiiiiiviD(A)(B)(C)(D)iiiviiii
A(A)(B)(C)(D)iiiviiiiB(A)(B)(C)(D)iiiiiiviC(A)(B)(C)(D)iiiiiiviD(A)(B)(C)(D)iiiviiiiMatch the List-I with List-II:
 A(I)(II)(III)(IV)1245B(I)(II)(III)(IV)5436C(I)(II)(III)(IV)2611D(I)(II)(III)(IV)6251
A(I)(II)(III)(IV)1245B(I)(II)(III)(IV)5436C(I)(II)(III)(IV)2611D(I)(II)(III)(IV)6251
Match the List -I with List - II.
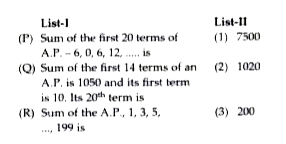
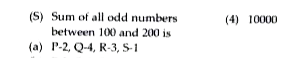
View SolutionMatch the statements given in List I with the values given in List II.

View SolutionMatch the statements in List I with the correct answer from List II.

View SolutionMatch the List-I with List-II :

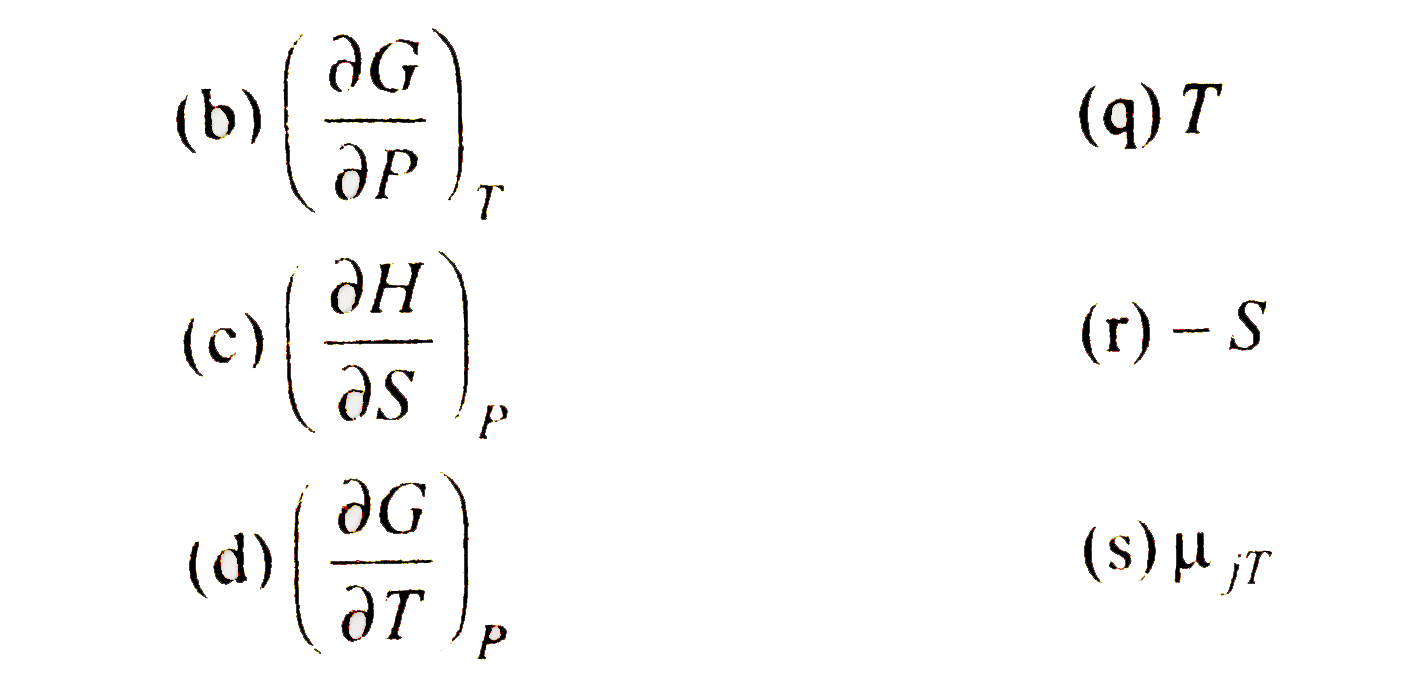
View SolutionMatch the list I with list II :
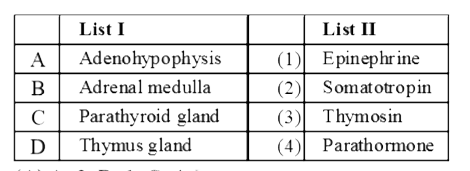
View Solution


