Let OABCD be a pentagon in which the sides OA and CB are parallel and the sides OD and AB are parallel as shown in figure. Also, OA:CB=2:1 and OD:AB=1:3. if the diagonals OC and AD meet at x, find OX:OC.
3/4
1/3
2/5
1/2
The correct Answer is:C
Let the position vectors of A, B, C and D be →a,→b,→cand→d, respectively. Then,
OA:CB=2:1
⇒−−→OA=2−−→CB
⇒→a=2(→b−→c) (i)
and OD:AB=1:3
3−−→OD=−−→AB
⇒3→d=(→b−→a)=→b−2(→b−→c) [ using(i)]
=−→b+2→c (ii)
Let OX:XC=λ:1andAX:XD=μ:1
Now, X divides OC in the ratio λ:1. Therefore,
P.VofX=λ→cλ+1 (iii)
X also divides AD in the ratio μ:1. Therefore,
P.V. of X = μ→d+→aμ+1 (iv)
From (iii) and (iv), we get
λ→cλ+1=μ→d+→aμ+1
or (λλ+1)→c=(μμ+1)→d+(1μ+1)→a
or (λλ+1)→c=(μμ+1)(−→b+2→c3)+(1μ+1)2(→b−→c)
[using (i) and (ii)]
or (λλ+1)→c=(6−μ3(μ+1))→b+(2μ3(μ+1)−2μ+1)→c
or (λλ+1)→c=(6−μ3(μ+1))→b+(2μ−63(μ+1))→c
or (6−μ3(μ+1))→b+(2μ−63(μ+1)−λλ+1)→c=→0
or 6−μ3(μ+1)=0and2μ−63(μ+1)−λλ+1=0
( as →band→c are non-collinear )
or μ=6,λ=25
Hence, OX:XC=2:5
Topper's Solved these Questions
- INTRODUCTION TO VECTORS BOOK - CENGAGE PUBLICATIONCHAPTER - INTRODUCTION TO VECTORS EXERCISE - MATRIX-MATCH TYPE
3 Videos
- INTRODUCTION TO VECTORS BOOK - CENGAGE PUBLICATIONCHAPTER - INTRODUCTION TO VECTORS EXERCISE - INTEGER TYPE
8 Videos
- INTRODUCTION TO VECTORS BOOK - CENGAGE PUBLICATIONCHAPTER - INTRODUCTION TO VECTORS EXERCISE - REASONING TYPE
11 Videos
- INTEGRALSBOOK - CENGAGE PUBLICATIONCHAPTER - INTEGRALSEXERCISE - All Questions
762 Videos
- INVERSE TRIGONOMETRIC FUNCTIONSBOOK - CENGAGE PUBLICATIONCHAPTER - INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - All Questions
541 Videos
Similar Questions
Let OABCD be a pentagon in which the sides OA and CB are parallel and the sides OD and AB are parallel as shown in figure. Also, OA:CB=2:1 and OD:AB=1:3. if the diagonals OC and AD meet at x, find OX:XC.
View SolutionLet OABCD be a pentagon in which the sides OA and CB are parallel and the sides OD and AB are parallel as shown in figure. Also, OA:CB=2:1 and OD:AB=1:3. if the diagonals OC and AD meet at x, find OX:XC.
View Solution
Knowledge Check
Length of parallel sides AB and CD of a trapezium are respectively 10 cm and 14 cm. If its diagonals AC and BD intersects at O then AO : OC is
A5:7B12:7C7:5D7:12
The side AB of a square ABCD is parallel to the x-axis. Find the slopes of all its sides.

Also, find :
the slope of the diagonal AC.
View SolutionThe side AB of a square ABCD is parallel to the x-axis. Find the slopes of all its sides.

Also, find :
the slope of the diagonal BD.
View SolutionIn the given figure if AOOC=BOOD=12and AB=5cm then find CD
View SolutionIn figure OAOC=OBOD=12and AB=5cm. Find the value of DC
View SolutionPerpendicular bisectors of the sides AB and AC of a triangle ABC meet at O.
What is the relation between the distances OA, OB and OC ?
View SolutionIn the following figure the radii (OA and OD) are 2 cm and △ABO and △DCO are right angle triangles. Also, OB=√2 cm and OC = 1 cm. Find the area of the shaded region in the circle.

View SolutionO is a point situated inside a rectangle ABCD. If sides OA, OC and OD are 6 cm, 8 cm and 6 cm respectively, then find the value of OB-
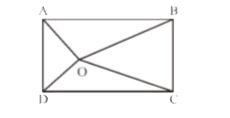
View Solution
