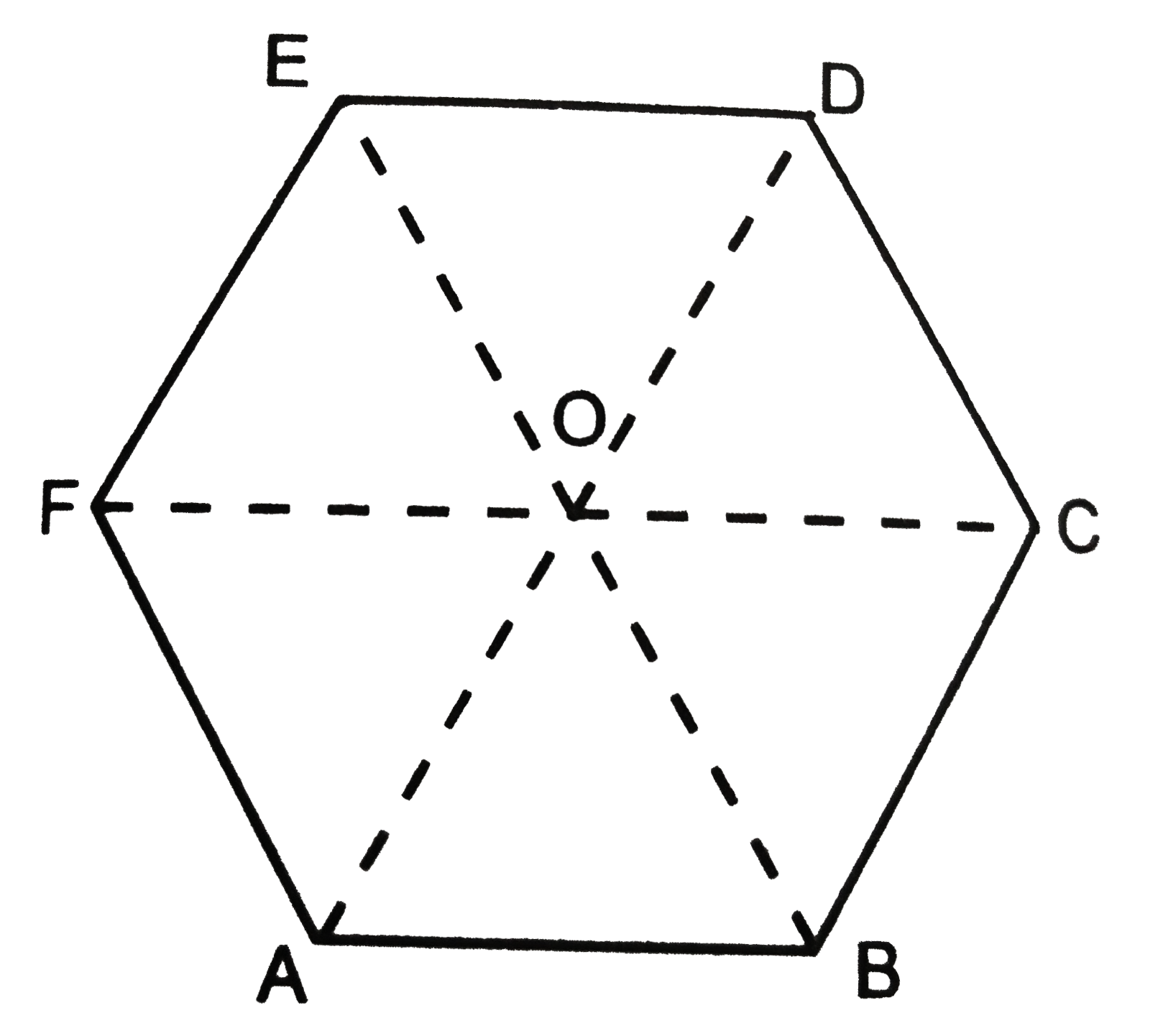
ABCDEF is a regular hexagon. Find the vector →AB+→AC+→AD+→AE+→AF in terms of the vector →AD
A
1
B
2
C
3
D
none of these
Text Solution
The correct Answer is:C

−−→AB+−−→AC+−−→AD+−−→AE+−−→AF
=−−→ED+−−→AC+−−→AD+−−→AE+−−→CD[∴−−→AB=→ED,→AF=→CD]
−−→AC+−−→CD+(−−→AE+−−→ED)+−−→AD
=−−→AD+−−→AD+−−→AD=3−−→AD
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
If ABCDEF is a regular hexagon , then A→D+E→B+F→C equals
A2A→BB→0C3A→BD4A→B
If ABCDEF is a regular hexagon then −−→AD+−−→EB+−−→FC equals :
View SolutionIf ABCDEF is a regualr hexagon, then −−→AC+−−→AD+−−→EA+−−→FA=
View SolutionIn a regular hexagon ABCDEF, −−→AE
View SolutionLet ABCDEF be a regular hexagon and −−→AB=→a,−−→BC=→b,−−→CD=→c then −−→AE is
View SolutionIf ABCDEF is a regular hexagon, them −−→AD+−−→EB+−−→FC equals
View SolutionIn a regular hexagon ABCDEF, −−→AE
View SolutionABCDEF is a regular hexagon, Fig. 2 (c ) .65. What is the value of
(−−→AB+−−→AC+−−→AD+−−→AE+−−→AF?
 .
.
View Solution
