Let S be a square of unit area. Consider any quadrilateral which has one vertex on each side of S. If a,b,candd denote the lengths of sides of the quadrilateral, prove that 2≤a2+b2+c2+d2≤4 Solution in Bengali
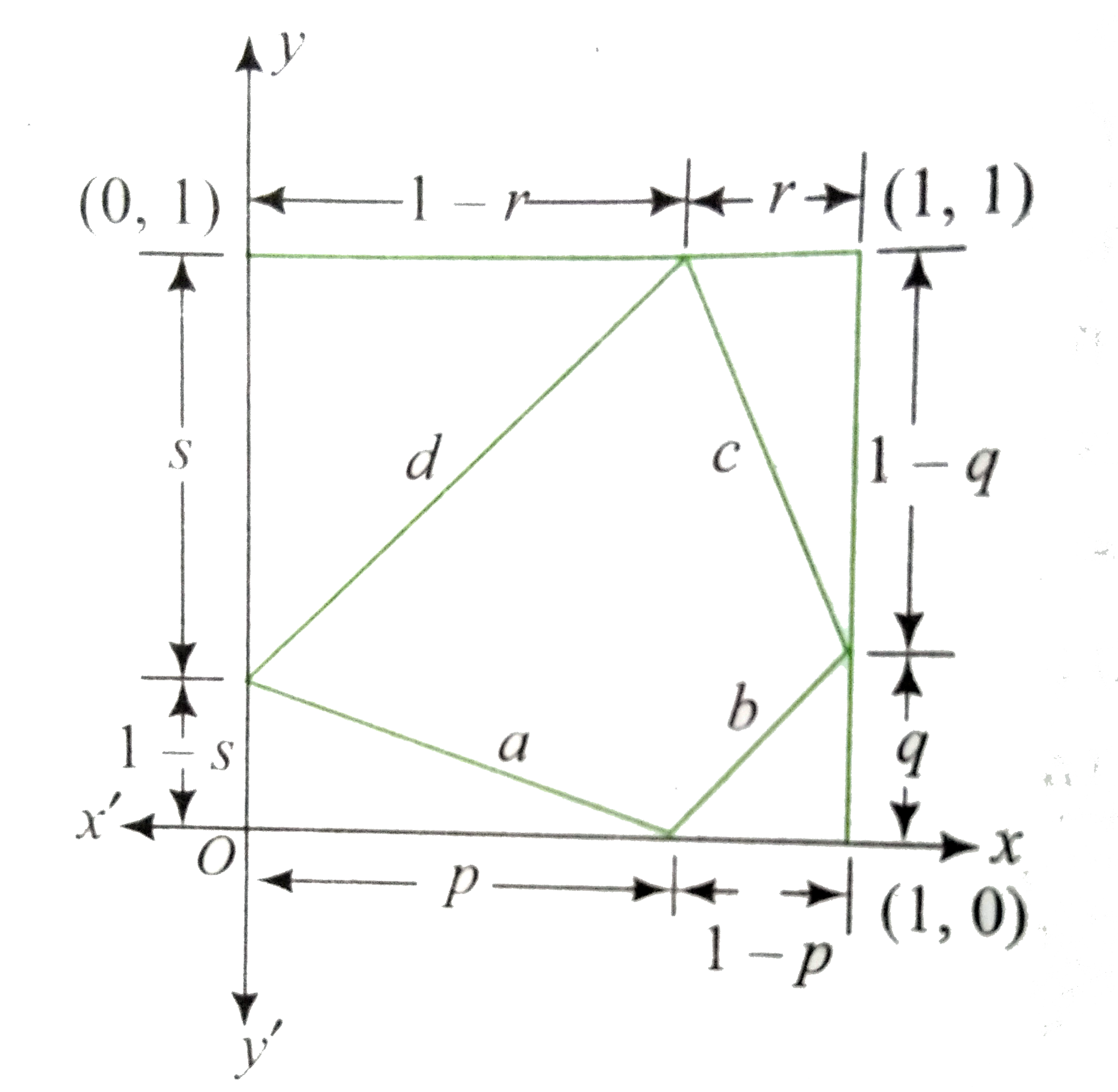
From the figure
a2=p2+(1−s)2
b^(2) = (1 - p)^(2) + q^(2)<br>a^(2) + b^(2) + c^(2) + d^(2)= [ p^(2) + (1 - p)^(2)] + [q^(2) + ( 1 - q)^(2) ] <br> [ r^(2) + (1 - r)^(2)] + [s^(2) + ( 1 - s)^(2) ],wherep,q,r,sin[0,1]<br>Nowconsrthefunction<br>y = x^(2) + (1 - x)^(2), 0 le x le 1<br>rArr y = 2x^(2) - 2x + 1 = 2 (x - (1)/(2))^(2) + (1)/(2)<br>Hence,miniμmvalueis1//2whenx=1//2andmaxiμmvalueisatx=1,whichis1.Therefore,miniμmvalueofa^(2) + b^(2) + c^(2) d^(2)is1//2+ 1//2 + 1//2 +1//2 = 2andmaxiμmvalueis1 + 1 + 1 + 1 = 4.
Topper's Solved these Questions
- THEORY OF EQUATIONSBOOK - CENGAGE PUBLICATIONCHAPTER - THEORY OF EQUATIONSEXERCISE - CONCEPT APPLICATION EXERCISE 2.1
3 Videos
- THEORY OF EQUATIONSBOOK - CENGAGE PUBLICATIONCHAPTER - THEORY OF EQUATIONSEXERCISE - CONCEPT APPLICATION EXERCISE 2.2
5 Videos
- THEORY OF EQUATIONSBOOK - CENGAGE PUBLICATIONCHAPTER - THEORY OF EQUATIONSEXERCISE - ILLUSTRATION
121 Videos
- STRAIGHT LINESBOOK - CENGAGE PUBLICATIONCHAPTER - STRAIGHT LINESEXERCISE - ARCHIVES (NUMERICAL VALUE TYPE)
1 Videos
- THREE DIMENSIONAL GEOMETRYBOOK - CENGAGE PUBLICATIONCHAPTER - THREE DIMENSIONAL GEOMETRYEXERCISE - All Questions
291 Videos
Similar Questions
If x=1andx=2 are solutions of equations x3+ax2+bx+c=0anda+b=1, then find the value of b.
View SolutionGiven that the expression 2x3+3px2−4x+p has a remainder of 5 when divided by x+2 , find the value of p.
View Solutionf(x) be a quadratic polynomial f(x)=(x−1)(ax+b) satisfying f(2)+f(4)=0.
If unity is one root of f(x) = 0 then find the other root.
View SolutionFor a point P in the plane, let d1(P)andd2(P) be the distances of the point P from the lines x−y=0andx+y=0 respectively. The area of the region R consisting of all points P lying in the first quadrant of the plane and satisfying 2≤d1(P)+d2(P)≤4, is
View SolutionFind the angle between the line whose direction cosines are given by l+m+n=0andl2+m2−n2=0.
View SolutionLet S be a square of nit area. Consider any quadrilateral, which has none vertex on each side of S. If a,b,candd denote the lengths of the sides of het quadrilateral, prove that 2≤a2+b2+c2+x2≤4.
View SolutionThe area of any cyclic quadrilateral ABCD is given by A2=(s−a)(s−b)(s−c)(s−d), where 2s=a+b++c+d,a,b,candd are the sides of the quadrilateral
Now consider a cyclic quadrilateral ABCD of area 1 sq. unit and answer the following question
The minium perimeter of the quadrilateral is
View SolutionThe area of any cyclic quadrilateral ABCD is given by A2=(s−a)(s−b)(s−c)(s−d), where 2s=a+b++c+d,a,b,candd are the sides of the quadrilateral
Now consider a cyclic quadrilateral ABCD of area 1 sq. unit and answer the following question
When the perimeter is minimum, the quadrilateral is necessarily
View SolutionLet S be the square of unit area. Consider any quadrilateral which has one vertex on each side of S. If a, b, c and d denote the lengths of the sides of the quadrilateral, prove that 2≤a2+b2+c2+d2≤4.
View SolutionLet S be a square of unit area. Consider any quadrilateral which has one vertex on each side of S. If a,b,c and d denote the lenghts of the sides of the quadrilateral,
Prove that 2≤a2+b2+c2+d2≤4.
View SolutionLet S be a square of unit area. Consider any quadrilateral which has one vertex on each side of S. If a,b,candd denote the lengths of sides of the quadrilateral, prove that 2≤a2+b2+c2+d2≤4
View SolutionThe area of any cyclic quadrilateral ABCD is given by A2=(s−a)(s−b)(s−c)(s−d), where 2s=a+b++c+d,a,b,candd are the sides of the quadrilateral
Now consider a cyclic quadrilateral ABCD of area 1 sq. unit and answer the following question
The minium perimeter of the quadrilateral is
View Solutionमाना इकाई क्षेत्रफल का एक वर्ग है। माना कोई चतुर्भुज जिसके शीर्ष वर्गकी प्रत्येक भुजा पर है। यदि a, b, c तथा d चतुर्भुज की भुजाओं की लम्बाई को दर्शाता है, तो सिद्ध कीजिए कि 2≤a2+b2+c2+d2≤4 होगा।
View SolutionThe area of any cyclic quadrilateral ABCD is given by A2=(s−a)(s−b)(s−c)(s−d), where 28 = a + b + c + d, a, b,c and d are the sides of the quadrilateral. Now consier a cyclic quadrilateral ABCD of area 1sq.unit and answer the following questions:
The minimum perimeter of the quadrilateral is
View SolutionThe area of any cyclic quadrilateral ABCD is given by A2=(s−a)(s−b)(s−c)(s−d), where 28 = a + b + c + d, a, b,c and d are the sides of the quadrilateral. Now consier a cyclic quadrilateral ABCD of area 1sq.unit and answer the following questions:
The minimum value of the sum of the lengths of diagonals
View SolutionThe area of any cyclic quadrilateral ABCD is given by A2=(s−a)(s−b)(s−c)(s−d), where 28 = a + b + c + d, a, b,c and d are the sides of the quadrilateral. Now consier a cyclic quadrilateral ABCD of area 1sq.unit and answer the following questions:
When the perimeter is minimum, the quadrilateral is necessarily
View Solution
