If $x^{4} + 2 k x^{3} + x^{2} + 2 k x + 1 = 0$
has exactly tow distinct positive and two distinct negative roots, then find the possible real values of k.

Text Solution

Verified by Experts

The given equation is $(x^{2} + \frac{1}{x^{2}}) + 2 k (x + \frac{1}{x}) + 1 = 0$
or ${(x + \frac{1}{x})}^{2} + 2 k (x + \frac{1}{x}) + 1 = 0$
Putting $x + \frac{1}{x} = t$ , the above equation to $t^{2} + 2 k t - 1 = 0$
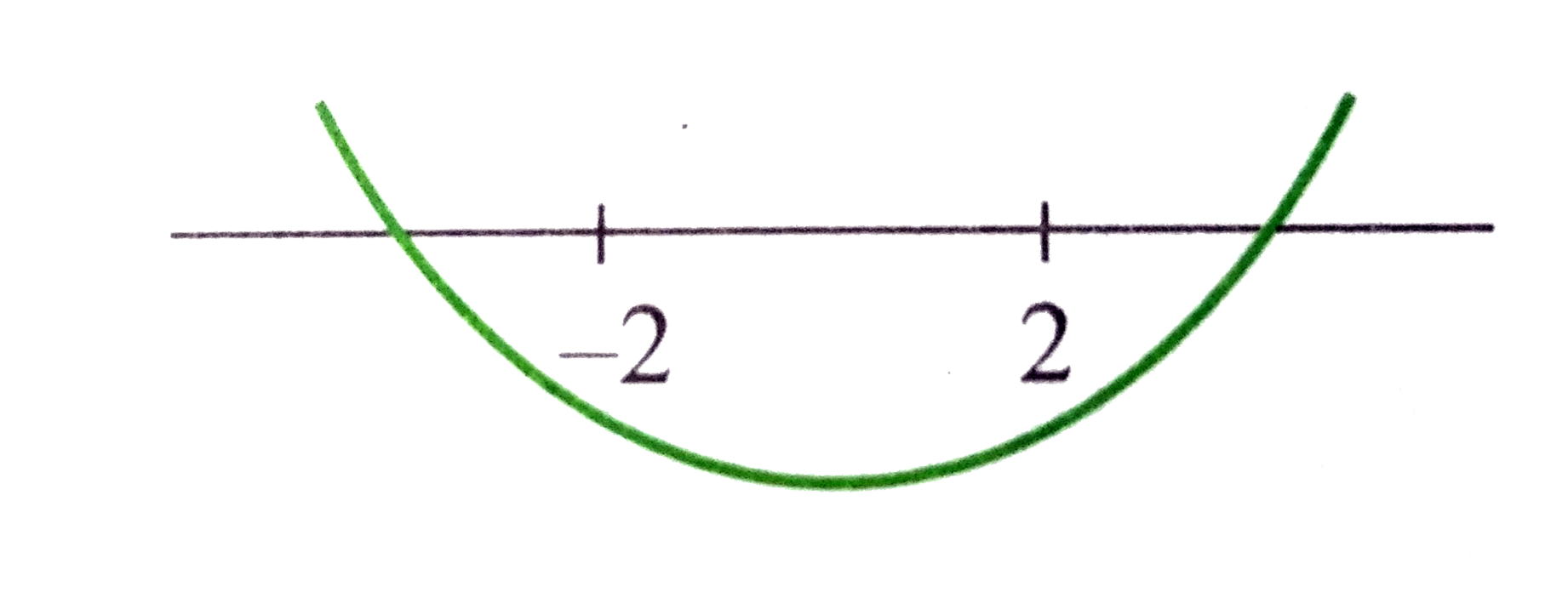
Now, we know that $x + \frac{1}{x} \geq 2 if x > 0, and x + \frac{1}{x} < - 2 if x < 0$ .
So, one of the rots of $t^{2} + 2 k t - 1 = 0$ will lie in $(- \infty, - 2)$ and other root in $(2, \infty)$ .
$∴ f (- 2) < 0$
$\Rightarrow 4 - 4 k - 1 < 0$
or $k > 3 / 4$
And $f (2) < 0$
$\Rightarrow 4 + 4 k - 1 < 0$
or $k < - 3 / 4$
Henc, k $\in ϕ .$

If the roots of $5 x^{2} - k x + 1 = 0$ are real and distinct then
A $- 2 \sqrt{5} < k < 2 \sqrt{5}$
B $k > 2 \sqrt{5}$ only
C $k < - 2 \sqrt{5}$ only
Deither $k > 2 \sqrt{5} or k < - 2 \sqrt{5}$
If the equation $3 x^{2} - 6 x + k = 0$ has real and distinct roots, then the value of k is
A $k \leq 3$
B $k = 3$
C $k > 3$
D $k < 3$