Consider the inequality 9x−a⋅3x−a+3≤0, where a is a real parameter.
The given inequality has at least one positive solution for a∈Solution in Bengali
(−∞,−2)
[3,∞)
(2,∞)
[−2,∞)
The correct Answer is:3
Given that 9x−a3x−a+3≤0
Let t=3x. Then,
t2−at−a+3≤0
or t3+3≤a(t+1) (1)
where t∈R+,∀x∈R
Let f1(t)=t2+3 and
f2(t)=a(t+1).
For at least one posititve solution, t∈(1,∞). That means graphs of f1(t)=t2+3andf2(t)=a(t+1) should meet at least once is t∈(1,∞). If a=2, both the curves touch each other at (1,4).
Hence, the required range is a∈(2,∞)
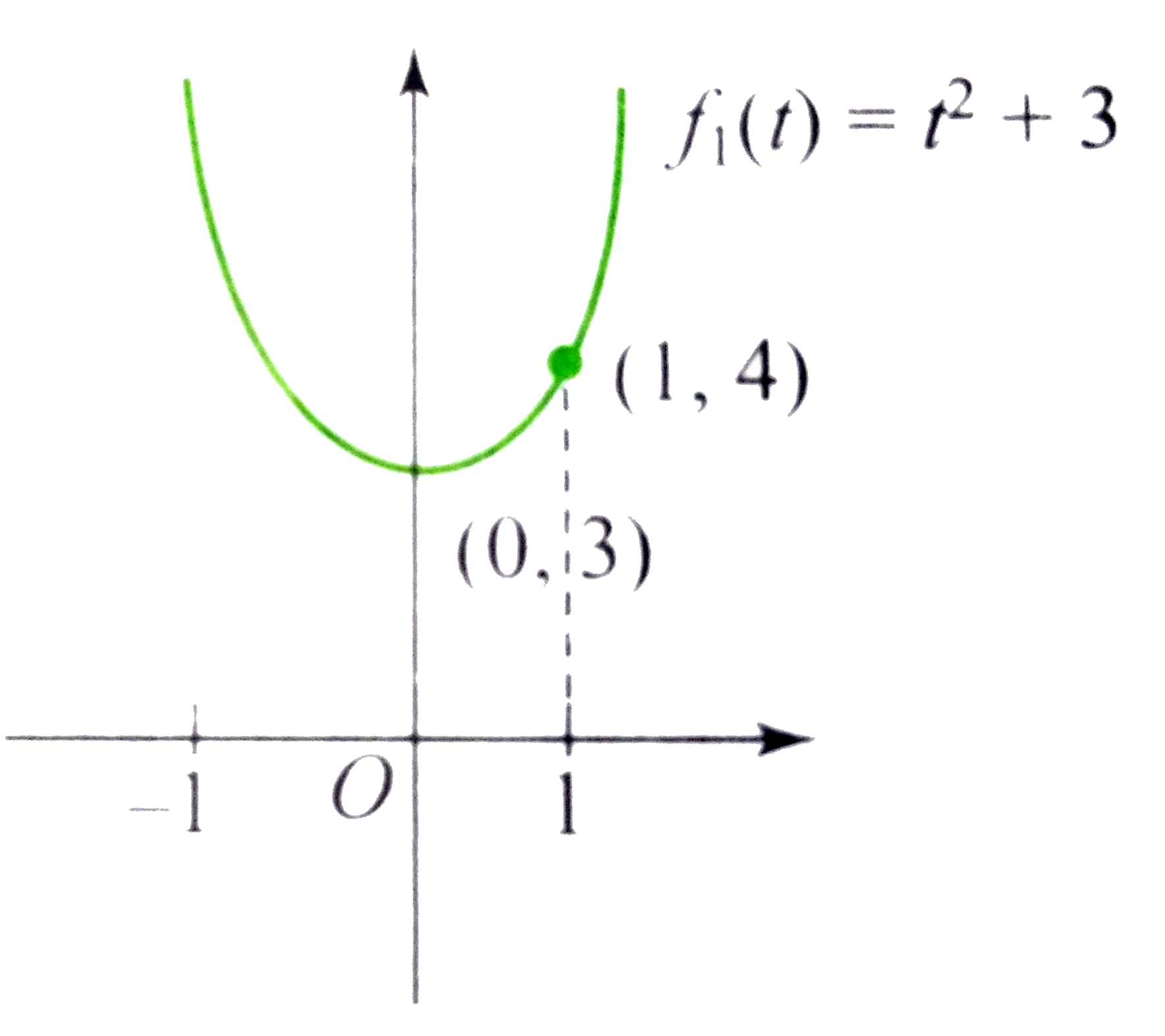
Topper's Solved these Questions
- BOOK - CENGAGE PUBLICATIONCHAPTER - THEORY OF EQUATIONSEXERCISE - MATRIX MATCH TYPE6videos
THEORY OF EQUATIONS
- BOOK - CENGAGE PUBLICATIONCHAPTER - THEORY OF EQUATIONSEXERCISE - NUMERICAL VALUE TYPE43videos
THEORY OF EQUATIONS
- BOOK - CENGAGE PUBLICATIONCHAPTER - THEORY OF EQUATIONSEXERCISE - Multiple Correct Answer Type38videos
THEORY OF EQUATIONS
- BOOK - CENGAGE PUBLICATIONCHAPTER - STRAIGHT LINESEXERCISE - ARCHIVES (NUMERICAL VALUE TYPE)1videos
STRAIGHT LINES
- BOOK - CENGAGE PUBLICATIONCHAPTER - THREE DIMENSIONAL GEOMETRYEXERCISE - All Questions291videos
THREE DIMENSIONAL GEOMETRY
Similar Questions
Match the following for the equation x2+a|x|+1=0 where, a is a parameter.
 View Solution
View SolutionIf x=2+22/3+21/3 , then the value of x3−6x2+6x is
01:23View SolutionIf c≠0 and the equation p2x=ax+c+bx−c has two equal roots, then p can be
02:27View SolutionFor a point P in the plane, let d1(P)andd2(P) be the distances of the point P from the lines x−y=0andx+y=0 respectively. The area of the region R consisting of all points P lying in the first quadrant of the plane and satisfying 2≤d1(P)+d2(P)≤4, is
02:50View SolutionFind the angle between the line whose direction cosines are given by l+m+n=0andl2+m2−n2=0.
03:10View SolutionConsider the inequality, 9x−a.3x−a+3≤0, where 'a' is a real parameter.
(a) Find the value of 'a' for which the inequality has at least one negative solution.
(b) Find the values of 'a' for which the inequality has at least one positive solution.
(c) Find the vlaues of 'a' for which the inequality has at least one real solution.02:28View SolutionConsider the inequation x2+x+a−9<0
The values of the real parameter a so that the given inequaiton has at least one positive solution:02:14View SolutionConsider the inequation x2+x+a−9<0
The values of the real parameter a so that the given inequations has at least one negative solution.03:51View SolutionConsider the inequation 9x−a3x−a+3≤0, where a is real parameter.
The given inequality has at least one negative soluiton for a∈02:47View SolutionConsider the inequation 9x−a3x−a+3≤0, where a is real parameter.
The given inequality has at least one real solutions for a∈.02:13View SolutionDraw the graphs of solutions sets of the following inequations:
x+2y−3≤002:50View SolutionFind the graph of linear inequation in xy plane x+4>0
02:12View SolutionConsider the inequality 9x−a.3x−a+3≤0 where 'a' is a real parameter.
The given inequality has at least one negative solution for 'a' lying in-02:57View SolutionFind the graph of linear inequation in xy plane 2y+7≤0
03:58View SolutionFind the graph of linear inequation in xy plane 4x+8>0
03:50View SolutionConsider the inequation 9x−a3x−a+3≤0, where a is real parameter.
The given inequality has at least one negative solution for a∈ (a) (−∞,2) (b) (3,∞) (c) (−2,∞) (d) (2,3)03:19View Solution

