lf abcd=1 where a,b,c,d are positive reals then the minimum value of a2+b2+c2+d2+ab+ac+ad+bc+bd+cd is Solution in Bengali
The correct Answer is:10
Given,abcd =1
We know that , AM≥GM
∴a2+b2+c2+d2+ab+ac+ad+bc+bd+cd10
≥[a2×b2×c2×d2×(ab)×(ac)×(ad)×(bc)×(bd)×(cd)]1/10
=(a5×b5×c5×d5)1/10
=(abcd)1/2
=(1)1/2
⇒a2b2+c2+d2+ab+ac+ad+bc+bd+cd10≥1
⇒a2+b2+c2+d2+ab+ac+ad+bc+bd+cd≥10.
Topper's Solved these Questions
- BOOK - CENGAGE PUBLICATIONCHAPTER - INEQUALITIES INVOLVING MEANS EXERCISE - Concept Application Eexercises 6.36videos
INEQUALITIES INVOLVING MEANS
- BOOK - CENGAGE PUBLICATIONCHAPTER - INEQUALITIES INVOLVING MEANS EXERCISE - Concept Application Eexercises 6.44videos
INEQUALITIES INVOLVING MEANS
- BOOK - CENGAGE PUBLICATIONCHAPTER - INEQUALITIES INVOLVING MEANS EXERCISE - Concept Application Eexercises 6.18videos
INEQUALITIES INVOLVING MEANS
- BOOK - CENGAGE PUBLICATIONCHAPTER - INEQUALITIES AND MODULUSEXERCISE - Single correct Answer21videos
INEQUALITIES AND MODULUS
- BOOK - CENGAGE PUBLICATIONCHAPTER - INTEGRALSEXERCISE - All Questions762videos
INTEGRALS
Similar Questions
Prove that [a2+b2a+b]a+b>aabb>{a+b2}a+b.
02:49View SolutionProve that a4+b4+c4>abc(a+b+c),wherea,b,c>0.
02:40View SolutionProve that 1a+1b+1c≥1√(bc)+1√(ca)+1√(ab), where a,b,c > 0
04:57View SolutionIf f(x)=ax2+bx+c and f(−1)≥−4, f(1)≤0 and f(3)≥5, then the least value of a is
04:50View SolutionIf ∫dxx2+ax+1=f(g(x))+c, then f(x) is inverse trigonometric function for |a|>2 f(x) is logarithmic function for |a|<2 g(x) is quadratic function for |a|>2 g(x) is rational function for |a|<2
02:23View SolutionIf abcd=1 where a,b,c,d are positive reals then the minimum value of a^(2)+b^(2)+c^(2)+d^(2)+ab+ac+ad+bc+bd+cd is
01:32View SolutionThe minimum value of (sqrt((A^(2)+A+1)(B^(2)+B+1)(C^(2)+C+1)(D^(2)+D+1)))/(ABCD) is quad (where A,B,C,D) are positive real numbers)
03:11View SolutionIf a,b,c and d are different positive real numbers in H.P,then (A)ab>cd(B)ac>bd (D) none of these (C)ad>bc
03:27View SolutionIn quadrilatcal ABCD,prove that AB+BC+CD+AD<2(BD+AC)
00:58View SolutionIf four sides of a quadrilateral ABCD are tangential to a circle, then AC+AD=BD+CD (b) AB+CD=BC+AD (c) AB+CD=AC+BC (d) AC+AD=BC+DB
04:10View SolutionIn the figure, seg AD⊥ side BC and B−D−C, then prove AB2−BD2=AC2−CD2.
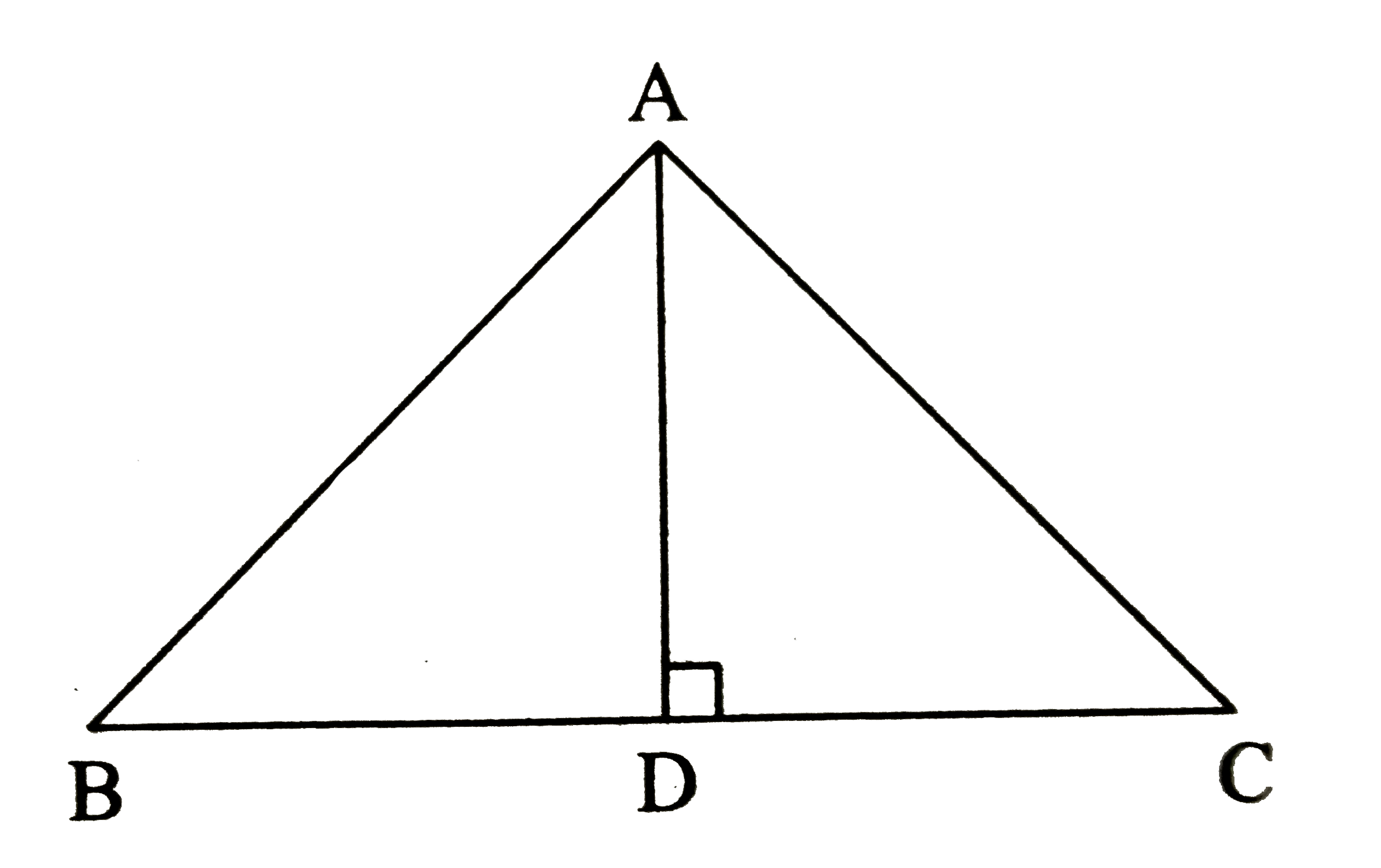 02:05View Solution
02:05View Solutionसिद्ध कीजिए कि:
∣∣∣ad+bcbd−acac−bdad+bc∣∣∣=(a2+b2)(c2+d2).01:59View Solutionयदि a,b,c,d गुणोत्तर श्रेणी में है, तो सिध्द कीजिए कि-
(a2+ac+c2)(b2+bd+d2)=(ab+bc+cd)2View SolutionIf a,b,c,d are positive numbers such that a,b,c are in A.P. and b,c,d are in H.P., then : (A) ab=cd (B) ac=bd (C) ad=bc (D)none of these
04:02View Solutionसिद्ध कीजिए कि: ∣∣∣ad+bcac−bdbd−acad+bc∣∣∣=(a2+b2)(c2+d2)
02:18View SolutionSuppose that a b c d are real numbers satisfying a≥b≥c≥d≥0 a2+d2=1andb2+c2=1 and ac+bd=13 .The value of ab-cd is
03:00View Solution

