If two parallel lines are cut by two distinct transversals, then the quadrilateral formed by these four lines will always be a:
parallelogram
rhombus
square
trapezium
The correct Answer is:D
To solve the problem, we need to analyze the situation where two parallel lines are intersected by two distinct transversals. Here’s the step-by-step solution:
Step 1: Identify the Parallel Lines
We start with two parallel lines, which we can label as line AB and line CD.
Hint: Remember that parallel lines never meet and are always the same distance apart.
Step 2: Identify the Transversals
Next, we introduce two distinct transversals that cut across these parallel lines. We can label these transversals as line EF and line GH.
Hint: Transversals are lines that intersect two or more other lines at different points.
Step 3: Form the Quadrilateral
The intersection of the two parallel lines (AB and CD) with the two transversals (EF and GH) creates a quadrilateral. The vertices of this quadrilateral can be labeled as points E, F, G, and H.
Hint: A quadrilateral is a four-sided polygon formed by connecting four points.
Step 4: Analyze the Properties of the Quadrilateral
Now, we need to determine the properties of the quadrilateral EFGH.
- Opposite Sides: We observe that EF is parallel to GH (because they are both formed by the intersection of the same pair of parallel lines), while EH is not parallel to FG (since they are transversals).
Hint: For a quadrilateral to be a parallelogram, both pairs of opposite sides must be parallel.
Step 5: Determine the Type of Quadrilateral
Since one pair of opposite sides (EF and GH) is parallel, but the other pair (EH and FG) is not, the quadrilateral EFGH fits the definition of a trapezium (or trapezoid in some regions), where only one pair of opposite sides is parallel.
Hint: A trapezium has one pair of parallel sides and the other pair is not parallel.
Conclusion
Thus, the quadrilateral formed by two parallel lines cut by two distinct transversals is always a trapezium.
Final Answer: The quadrilateral formed by these four lines will always be a trapezium.
We start with two parallel lines, which we can label as line AB and line CD.
Next, we introduce two distinct transversals that cut across these parallel lines. We can label these transversals as line EF and line GH.
The intersection of the two parallel lines (AB and CD) with the two transversals (EF and GH) creates a quadrilateral. The vertices of this quadrilateral can be labeled as points E, F, G, and H.
Now, we need to determine the properties of the quadrilateral EFGH.
Hint: For a quadrilateral to be a parallelogram, both pairs of opposite sides must be parallel.
Since one pair of opposite sides (EF and GH) is parallel, but the other pair (EH and FG) is not, the quadrilateral EFGH fits the definition of a trapezium (or trapezoid in some regions), where only one pair of opposite sides is parallel.
Thus, the quadrilateral formed by two parallel lines cut by two distinct transversals is always a trapezium.
Topper's Solved these Questions
- BOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - POLYGONS AND QUADRILATERALSEXERCISE - Self Assessment Sheet10videos
POLYGONS AND QUADRILATERALS
- BOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - POLYGONS AND QUADRILATERALSEXERCISE - Self Assessment Sheet10videos
POLYGONS AND QUADRILATERALS
- BOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - PERIMETER AND AREA EXERCISE - SELF ASSESSMENT SHEET10videos
PERIMETER AND AREA
- BOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - POWERS AND ROOTS EXERCISE - UNIT TEST-120videos
POWERS AND ROOTS
Similar Questions
Knowledge Check
- Question 1 - Select One
If two parallel lines are cut by a transversal, then the alternate interior angles are equal
ATRUEBFALSECCannot be determinedDNone of these - Question 2 - Select One
Two parallel line l and m are intersected by a transversal p. The quadrilateral formed by the bisectors of interior angles is a
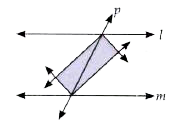 ATrapeziumBKiteCParallelogramDSquare
ATrapeziumBKiteCParallelogramDSquare - Question 3 - Select One
If two parallel lines are intersected by a transversal , then the interior angles on the same side of the transversal are -
AequalBadjacentCSupplementaryDComplementary
Which of the following statements are true (T) and which are false (F)? Give reasons. (i)If two lines are intersected by a transversal, then corresponding angles are equal. (ii)If two parallel lines are intersected by a transversal, then alternate interior angles are equal. (iii)Two lines perpendicular to the same line are perpendicular to each other. (iv)Two lines parallel to the same line are parallel to each other. (v)If two parallel lines are intersected by a transversal, then the interior angle on the same side of the transversal are equal.
View SolutionTwo parallel lines l and m are intersected by a transversal p (see Fig. 8.15). Show that the quadrilateral formed by the bisectors of interior angles is a rectangle.
View SolutionIf two parallel lines are intersected by a transversal, prove that the bisectors of the two pairs of interior angles enclose a rectangle.
View SolutionIf three or more parallel lines are intersected by two transversal; Prove that the intercepts made by them on tranversal are propotional.
View SolutionFill in the blanks in each of the following to make the statement true: (i) If two parallel lines are intersected by a transversal, then each pair of corresponding angles are.... (ii) If two parallel lines are intersected by a transversal, then interior angles on the same side of the transversal are... (iii) Two lines perpendicular to the same line are.... to each other. (iv) Two lines parallel to the same line are .......... to each other. (v) If a transversal intersects a pair of lines in such away that a pair of alternate angles are equal, then the line are... (vi) If a transversal intersects a pair of lines in such away that the sum of interior angles on the same side of transversal is 180,then the line are .......
View Solution

