Which of the following pairs of lines can be parallel ?
1. Two tangents to a circle.
2. Two diameters of a circle.
3. A chord of circle and a tangent to a tangent to a circle.
4. Two chords of a circle.
Select the correct answer using the codes given below :
1, 2 and 3
2, 3 and 4
1, 3 and 4
1, 2 and 4
The correct Answer is:C
To determine which pairs of lines can be parallel among the given options, let's analyze each condition step by step.
Step 1: Analyze Two Tangents to a Circle
- Explanation: When two tangents are drawn from an external point to a circle, they can be parallel if they are drawn from points that are equidistant from the center of the circle.
- Conclusion: This condition can be satisfied, so two tangents to a circle can be parallel.
Step 2: Analyze Two Diameters of a Circle
- Explanation: A diameter of a circle always passes through the center. Therefore, any two diameters will intersect at the center of the circle.
- Conclusion: This condition cannot be satisfied, so two diameters of a circle cannot be parallel.
Step 3: Analyze a Chord of a Circle and a Tangent to a Circle
- Explanation: A tangent to a circle is always perpendicular to the radius at the point of tangency. A chord can be parallel to a tangent if it is drawn in such a way that it does not intersect the tangent line.
- Conclusion: This condition can be satisfied, so a chord of a circle and a tangent to a circle can be parallel.
Step 4: Analyze Two Chords of a Circle
- Explanation: Two chords can be drawn in a circle, and there are configurations where they can be parallel. For example, if both chords are drawn horizontally or vertically within the circle.
- Conclusion: This condition can be satisfied, so two chords of a circle can be parallel.
Final Conclusion
Based on the analysis:
1. Two tangents to a circle: Can be parallel
2. Two diameters of a circle: Cannot be parallel
3. A chord of a circle and a tangent to a circle: Can be parallel
4. Two chords of a circle: Can be parallel
Thus, the correct answer is that pairs of lines that can be parallel are: 1st, 3rd, and 4th.
- Explanation: When two tangents are drawn from an external point to a circle, they can be parallel if they are drawn from points that are equidistant from the center of the circle.
- Conclusion: This condition can be satisfied, so two tangents to a circle can be parallel.
- Explanation: A diameter of a circle always passes through the center. Therefore, any two diameters will intersect at the center of the circle.
- Conclusion: This condition cannot be satisfied, so two diameters of a circle cannot be parallel.
- Explanation: A tangent to a circle is always perpendicular to the radius at the point of tangency. A chord can be parallel to a tangent if it is drawn in such a way that it does not intersect the tangent line.
- Conclusion: This condition can be satisfied, so a chord of a circle and a tangent to a circle can be parallel.
- Explanation: Two chords can be drawn in a circle, and there are configurations where they can be parallel. For example, if both chords are drawn horizontally or vertically within the circle.
- Conclusion: This condition can be satisfied, so two chords of a circle can be parallel.
Based on the analysis:
1. Two tangents to a circle: Can be parallel
2. Two diameters of a circle: Cannot be parallel
3. A chord of a circle and a tangent to a circle: Can be parallel
4. Two chords of a circle: Can be parallel
Topper's Solved these Questions
- BOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - CIRCLES EXERCISE - SELF ASSESSMENT SHEET10videos
CIRCLES
- BOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - CIRCLES EXERCISE - UNIT TEST20videos
CIRCLES
- BOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - CIRCLES EXERCISE - UNIT TEST20videos
CIRCLES
- BOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - AVERAGE EXERCISE - UNIT TEST -320videos
AVERAGE
- BOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - CIRCUMFERENCE AND AREA OF A CIRCLE EXERCISE - SELF ASSESSMENT SHEET - 2210videos
CIRCUMFERENCE AND AREA OF A CIRCLE
Similar Questions
Knowledge Check
- Question 1 - Select One
If a chord of a circle of radius 5 cm is a tangent to another circle of radius 3 cm, both the circles being concentric, then the length of the chord is
A10 cmB12.5 cmC8 cmD7 cm - Question 2 - Select One
A chord of a circle is equal to its radius. A tangent is drawn to the circle at an extremity of the chord. The angle between the tangent and the chord is
A30∘B45∘C60∘D75∘
Prove that, if a diameter of a circle bisects two chords of the circle then those two chords are parallel to each other.
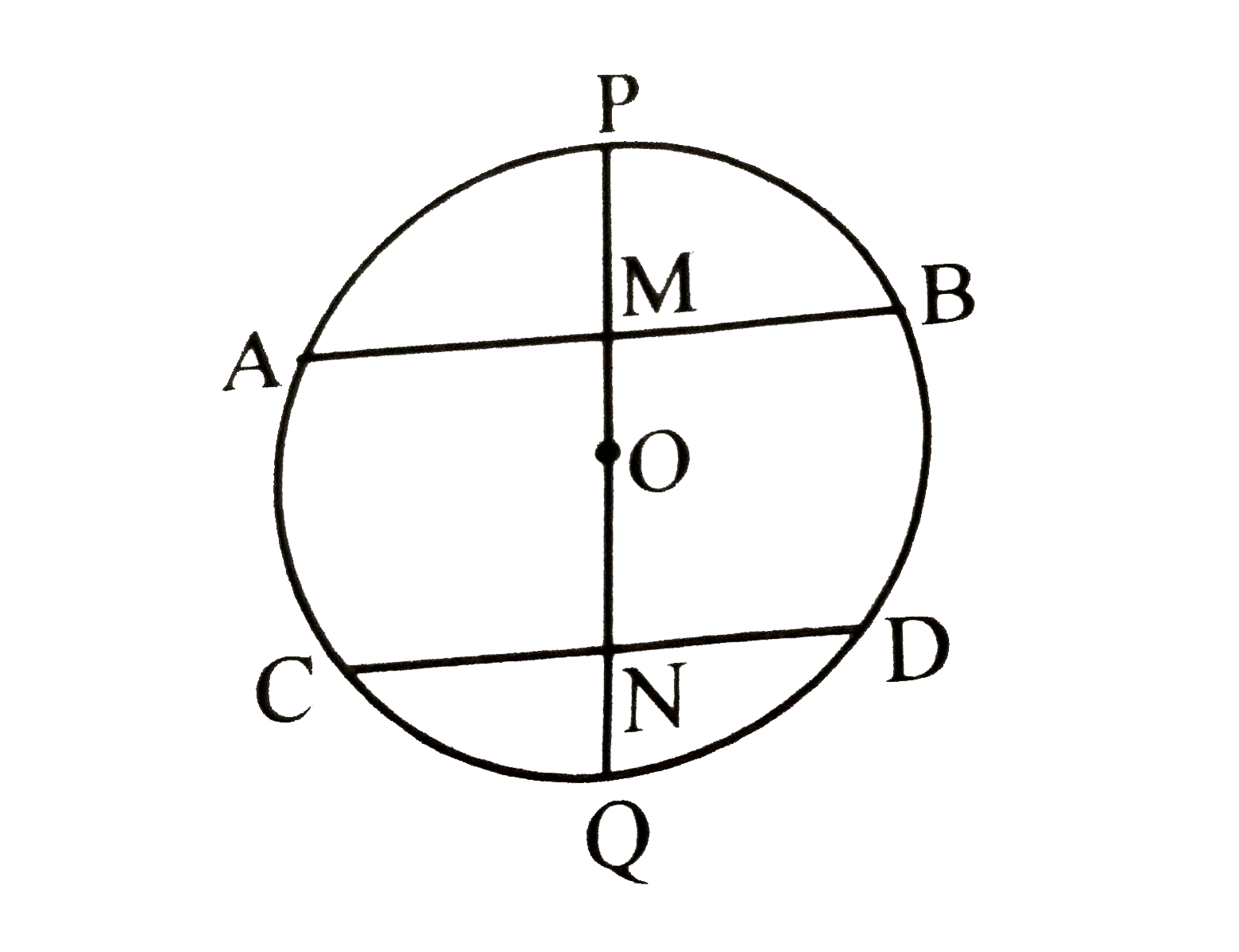 View Solution
View SolutionProve that a diameter AB of a circle bisects all those chords which are parallel to the tangent at the point A.
View SolutionIf a diameter of a circle bisects each of the two chords of a circle, prove that the chords are parallel.
View SolutionIf a diameter of a circle bisects each of the two chords of a circle, prove that the chords are parallel.
View SolutionOut of two concentric circles, the diameter of the outer circle is 26 cm and the chord MN of length 24 cm is tangent to the inner circle. The radius of the inner circle is
View SolutionA chord PQ of a circle is parallel to the tangent drawn at a point R of the circle,Prove that R bisects the arc PRQ.
View Solution

