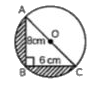
X and Y are the centres of 2 circles on a square as shown in the figure. What is the area of the shaded portion ? (Take π=3.14)
25.12cm2
28.26cm2
71.74cm2
88cm2
The correct Answer is:C
Step by step video, text & image solution for X and Y are the centres of 2 circles on a square as shown in the figure. What is the area of the shaded portion ? (Take pi = 3.14) by Maths experts to help you in doubts & scoring excellent marks in Class 7 exams.
Topper's Solved these Questions
- BOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - CIRCUMFERENCE AND AREA OF A CIRCLE EXERCISE - SELF ASSESSMENT SHEET - 2210videos
CIRCUMFERENCE AND AREA OF A CIRCLE
- BOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - CIRCUMFERENCE AND AREA OF A CIRCLE EXERCISE - SELF ASSESSMENT SHEET - 2210videos
CIRCUMFERENCE AND AREA OF A CIRCLE
- BOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - CIRCLES EXERCISE - UNIT TEST20videos
CIRCLES
- BOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - DATA HANDLING EXERCISE - Self Assessment Sheet - 2410videos
DATA HANDLING
Similar Questions
Knowledge Check
- Question 1 - Select One
The area of the shaded portion in the figure is
 A7.5π square unitsB6.5π square unitsC5.5π square unitsD4.5π square units
A7.5π square unitsB6.5π square unitsC5.5π square unitsD4.5π square units - Question 2 - Select One
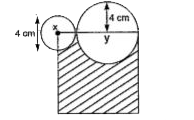
The figures in the rectangle are 8 identical quadrants. What is the area of the shaded part ? (Take π=3.14)
 A22.52cm2B15.48cm2C56.52cm2D28.36cm2
A22.52cm2B15.48cm2C56.52cm2D28.36cm2
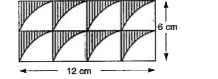
In figure, find the area of the shaded region [Useπ=3.14]
View SolutionThe given figure shows a circle inscribed in a square of side 14 cm.

What is the area of the shaded region?View SolutionQ.49 The area of the shaded portion in the given figure is
View SolutionAOBC is a quadrant of a circle of radius 10 cm. Calculate the area of the shaded portion. (Use π=3.14)
 View Solution
View SolutionIn the given figure, four equal circles are described about corners of a square so that each circle touches two of the circles as shown in the figure. Find the area of the shaded region, each side of the square measuring 14 cm.
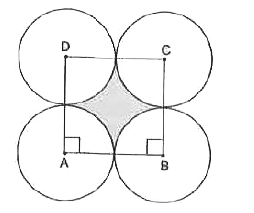 View Solution
View SolutionThe radius of each circle is 'a'. Then the area of the shaded portion is :
 View Solution
View Solution