If a triangle of base 6 cm has the same area as that of a circle of radius 6 cm, then the altitude of the triangle is
6π cm
8πcm
10πcm
12π cm
The correct Answer is:D
To solve the problem, we need to find the altitude of a triangle that has the same area as a circle with a radius of 6 cm. Let's break this down step by step.
Step 1: Calculate the area of the circle.
The formula for the area of a circle is given by:
Area of Circle=π×r2
where r is the radius. Here, the radius r=6 cm.
Substituting the value of the radius:
Area of Circle=π×(6)2=π×36=36π cm2
Step 2: Set up the equation for the area of the triangle.
The formula for the area of a triangle is:
Area of Triangle=12×base×height
Here, the base of the triangle is given as 6 cm, and we need to find the height (altitude), which we will denote as h.
Substituting the base into the formula:
Area of Triangle=12×6×h=3h cm2
Step 3: Set the areas equal to each other.
Since the area of the triangle is equal to the area of the circle, we can set the two equations equal:
3h=36π
Step 4: Solve for the height h.
To find h, we divide both sides of the equation by 3:
h=36π3=12π cm
Final Answer:
The altitude of the triangle is 12π cm.
---
The formula for the area of a circle is given by:
Area of Circle=π×r2
where r is the radius. Here, the radius r=6 cm.
Area of Circle=π×(6)2=π×36=36π cm2
The formula for the area of a triangle is:
Area of Triangle=12×base×height
Here, the base of the triangle is given as 6 cm, and we need to find the height (altitude), which we will denote as h.
Area of Triangle=12×6×h=3h cm2
Since the area of the triangle is equal to the area of the circle, we can set the two equations equal:
3h=36π
To find h, we divide both sides of the equation by 3:
h=36π3=12π cm
The altitude of the triangle is 12π cm.
Topper's Solved these Questions
- BOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - CIRCUMFERENCE AND AREA OF A CIRCLE EXERCISE - SELF ASSESSMENT SHEET - 2210videos
CIRCUMFERENCE AND AREA OF A CIRCLE
- BOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - CIRCUMFERENCE AND AREA OF A CIRCLE EXERCISE - SELF ASSESSMENT SHEET - 2210videos
CIRCUMFERENCE AND AREA OF A CIRCLE
- BOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - CIRCLES EXERCISE - UNIT TEST20videos
CIRCLES
- BOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - DATA HANDLING EXERCISE - Self Assessment Sheet - 2410videos
DATA HANDLING
Similar Questions
A circulare arc has been with vertex of an equilateral triangle of side 12 cm. The radius of arc is 6 cm. A sector of circle of radius 6 cm is cut from the triangle OAB. Find the area of the shaded region
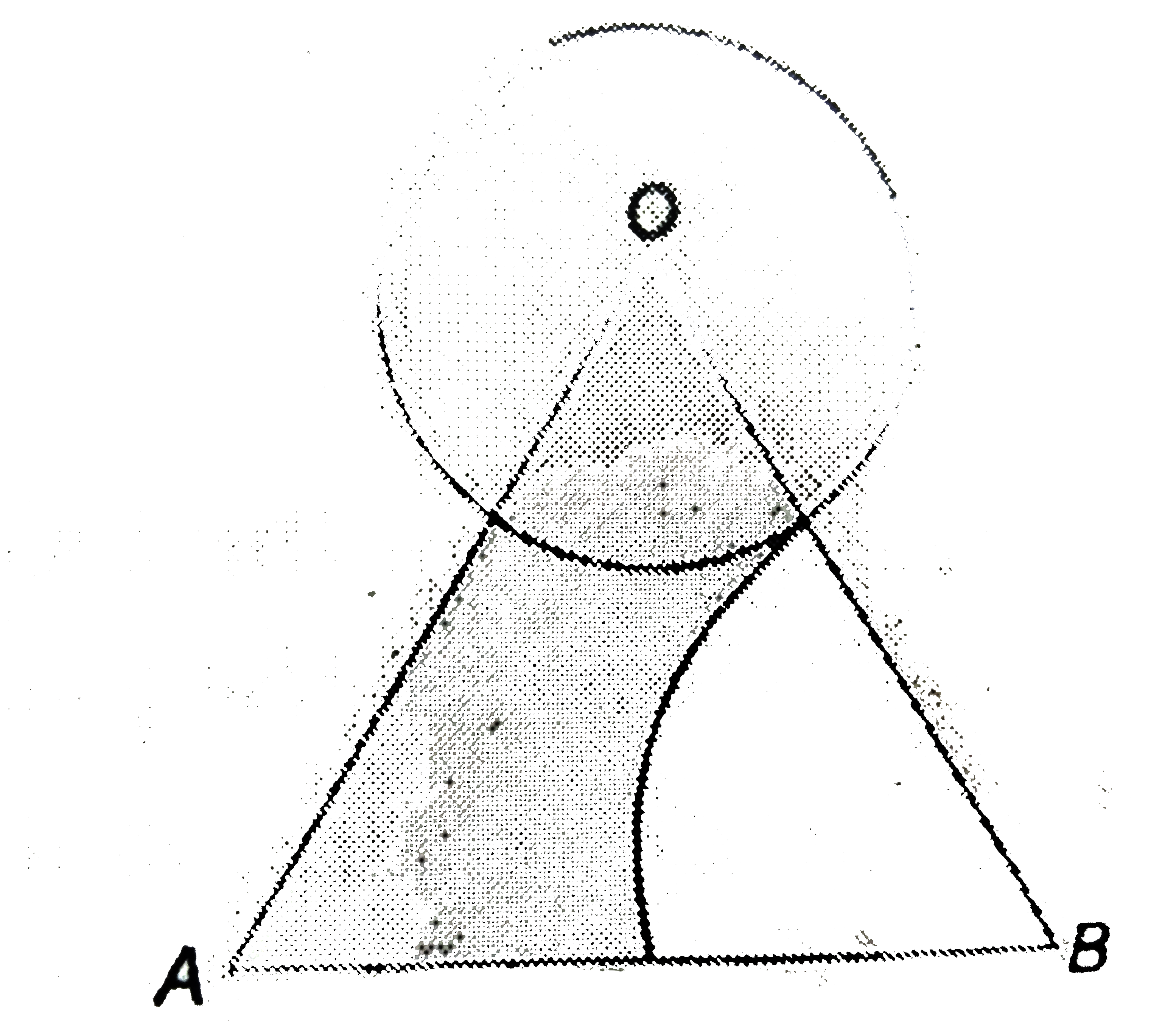 View Solution
View SolutionIf the area of a triangle is 1176 cm2 and base : corresponding altitude is 3 : 4, then the altitude of the triangle is (a) 42 cm (b) 52 cm (c) 54 cm (d) 56 cm
View Solution
Knowledge Check
- Question 1 - Select One
If a triangle with base 8 cm has the same area as a circle with radius 8 cm, then the corresponding altitude (in cm) of the triangle is
A12πB20πC16πD32π - Question 2 - Select One
If the area of triangle with base 12 cm is equal to the area of a square with side 12 cm, then the altitude of the triangle is:
A12 cmB24 cmC18 cmD36 cm - Question 3 - Select One
The height of an equilateral triangle is 6cm, then the area of the triangle is
A9√3cm2B3√3cm2C12√3cm2D17√3cm2
If the lengths of the sides of a triangle are in the ratio 4:5:6 and the inradius of the triangle is 3 cm, then the altitude of the triangle corresponding to the largest side as base is :
View SolutionIf the lengths of the sides of a triangle are in the ratio 4:5:6 and the inradius of the triangle is 3 cm, then the altitude of the triangle corresponding to the largest side as base is :
View SolutionThe height of an equilateral triangle is 6cm. Then the area of the triangle is
View SolutionA triangle and a parallelogram are constructed on the same base such that their areas are equal. If the altitude of the parallelogram is 100m, then the altitude of the triangle is 10√2m (b) 100m (c) 100√2m (d) 200m
View SolutionIf the area of a triangle is 1176cm2 and base : corresponding altitude is 3:4, then the altitude of the triangle is:
View Solution

