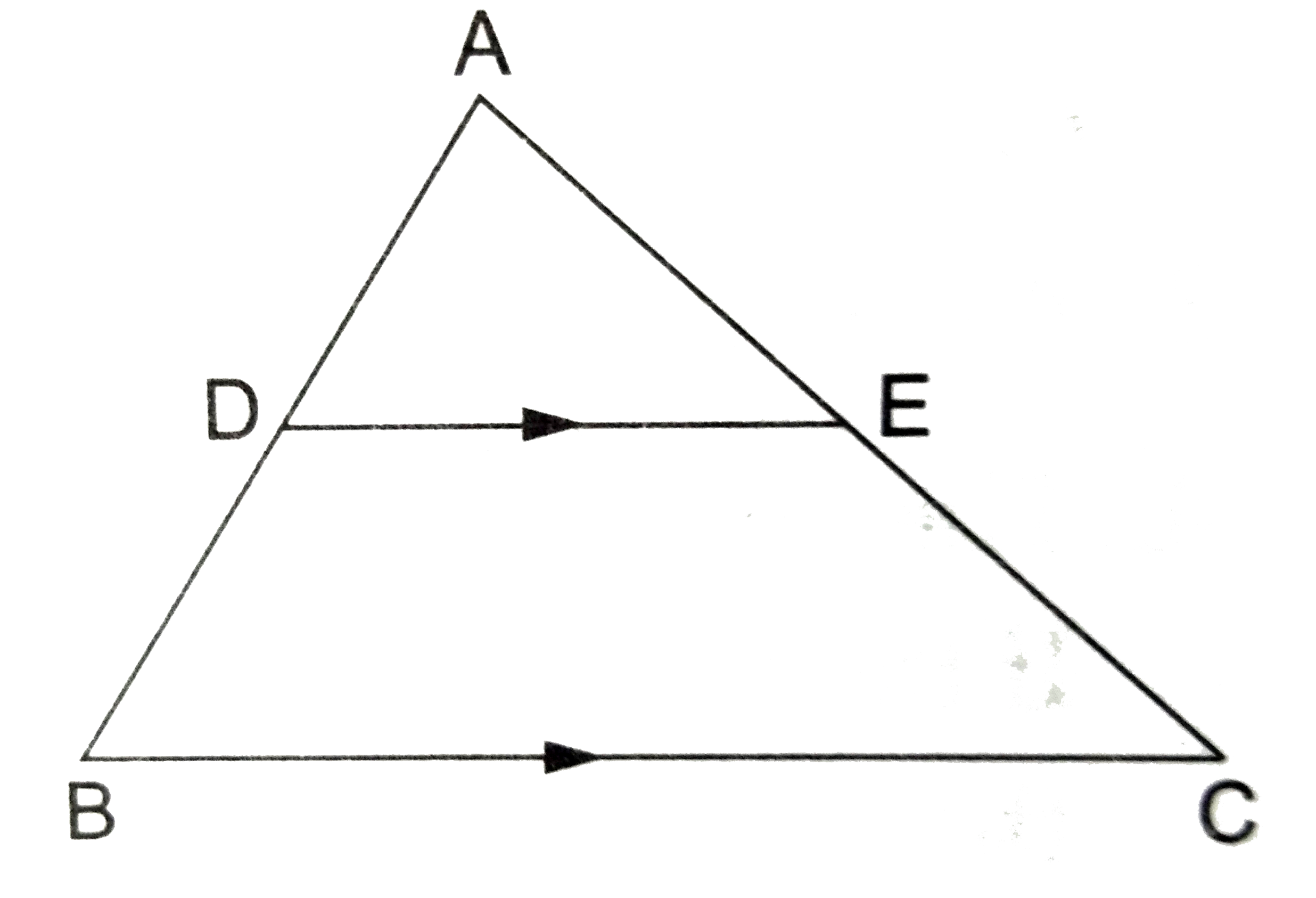
In the given figure, DE is parallel to BC and the ratio of the areas of ΔADE and trapezium BDEC is 4:5. What is DE: BC?
1:2
2:3
4:5
None of these
The correct Answer is:B
To solve the problem step by step, we will follow the reasoning presented in the video transcript.
1. Understanding the Given Information:
We have two parallel lines, DE and BC. The areas of triangle ADE and trapezium BDEC are given in the ratio of 4:5.
2. Setting Up the Ratios:
Let the area of triangle ADE be AADE=4x and the area of trapezium BDEC be ABDEC=5x.
3. Finding the Total Area:
The total area of triangle ABC can be expressed as:
AABC=AADE+ABDEC=4x+5x=9x
4. Using the Area Ratio of Similar Triangles:
Since DE is parallel to BC, triangle ADE is similar to triangle ABC. The ratio of their areas is equal to the square of the ratio of their corresponding sides:
AADEAABC=(DEBC)2
Substituting the areas we found:
4x9x=(DEBC)2
Simplifying this gives:
49=(DEBC)2
5. Taking the Square Root:
To find the ratio of DE to BC, we take the square root of both sides:
DEBC=√49=23
6. Final Ratio:
Thus, the ratio of DE to BC is:
DE:BC=2:3
We have two parallel lines, DE and BC. The areas of triangle ADE and trapezium BDEC are given in the ratio of 4:5.
Let the area of triangle ADE be AADE=4x and the area of trapezium BDEC be ABDEC=5x.
The total area of triangle ABC can be expressed as:
AABC=AADE+ABDEC=4x+5x=9x
Since DE is parallel to BC, triangle ADE is similar to triangle ABC. The ratio of their areas is equal to the square of the ratio of their corresponding sides:
AADEAABC=(DEBC)2
Substituting the areas we found:
4x9x=(DEBC)2
Simplifying this gives:
49=(DEBC)2
To find the ratio of DE to BC, we take the square root of both sides:
DEBC=√49=23
Thus, the ratio of DE to BC is:
DE:BC=2:3
Topper's Solved these Questions
- TRIANGLES BOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - TRIANGLES EXERCISE - Self Assessment Sheet
10 Videos
- TRIANGLES BOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - TRIANGLES EXERCISE - Self Assessment Sheet
10 Videos
- TIME AND WORK BOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - TIME AND WORK EXERCISE - Self Assessment Sheet - 20
10 Videos
- TRIGONOMETRICAL RATIOS BOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - TRIGONOMETRICAL RATIOS EXERCISE - Self Assessment Sheet - 40
1 Videos
Similar Questions
Knowledge Check
In the adjacent figure DE is parallel to BC and ratio of areas of ΔADE and trapezium BDEC is 4 : 5. What is the value of DE : BC?
 A1:2B2:3C4:5DNone of these
A1:2B2:3C4:5DNone of theseIn figure, if DE||BC, then find the ratio of ar (ΔADE) and ar(DECB).
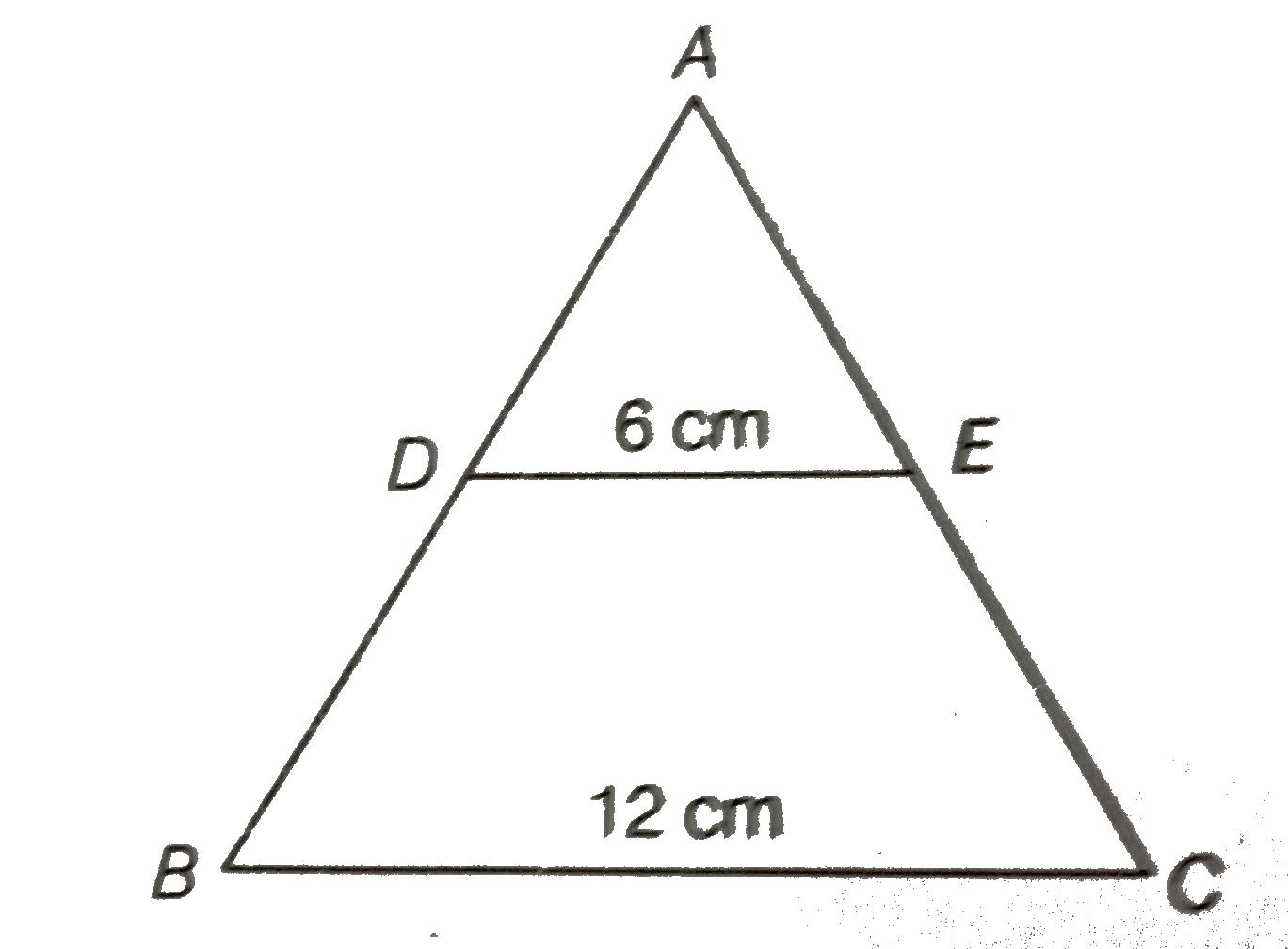 A1:3B1:2C2:5D3:5
A1:3B1:2C2:5D3:5
In the given figure DE∣∣BC find x,y,z
View SolutionIn the given figure if DE|| BC . Then EC =
View SolutionIn the given figure, if DE∣∣BC, then find the ratio of area of (△ADE) and (□DECB).
View SolutionIn the figure, DE∣∣BC. If AD=1cm and BD=2cm, then the ratio of areas of ΔADEandΔABC is
View SolutionIn the adjoining figure, DE is parallel to BC and AD=1cm, BD=2cm. What is the ratio of the area of ABC to the area of ADE?
View SolutionIn the figure, if DE∣∣BCandAD:AB=5:9, then the ratio of areas of ΔDEFandΔBFC is
View Solution