ΔABC is right angled at A and AD⊥BC. Then BDDC=
(ABAC)2
ABAC
(ABAD)2
ABAD
The correct Answer is:B
To solve the problem, we need to find the ratio BDDC in triangle ΔABC where A is the right angle and AD is perpendicular to BC.
1. Draw the Triangle:
- Begin by sketching triangle ABC with A at the right angle. Label the points as follows: A (right angle), B, and C.
- Draw a line segment BC and mark point D on BC such that AD is perpendicular to BC.
Hint: Visualizing the problem with a diagram helps in understanding the relationships between the angles and sides.
2. Identify Similar Triangles:
- Observe that triangles ABD and ACD are formed by the altitude AD.
- The angles in these triangles can be noted: ∠ADB=∠ABC (common angle), ∠ABD=∠ACD (both are right angles).
Hint: Look for common angles to establish similarity between triangles.
3. Apply AA Similarity Criterion:
- Since both triangles share angle A and both have a right angle, by the AA (Angle-Angle) similarity criterion, we can conclude that △ABD∼△ACD.
Hint: Remember that if two angles of one triangle are equal to two angles of another triangle, the triangles are similar.
4. Set Up Proportions:
- From the similarity of the triangles, we can write the proportion:
ABAC=BDDC
Hint: When triangles are similar, the ratios of their corresponding sides are equal.
5. Cross-Multiply:
- Rearranging the proportion gives:
BD=ABAC⋅DC
Hint: Cross-multiplication is a useful technique to manipulate proportions.
6. Express BDDC:
- To find BDDC, we can rearrange the equation:
BDDC=ABAC
Hint: Isolate the variable of interest to find the desired ratio.
7. Conclusion:
- The final result is:
BDDC=ABAC
Hint: Always double-check your final answer against the problem requirements.
Final Answer:
The ratio BDDC is equal to ABAC.
- Begin by sketching triangle ABC with A at the right angle. Label the points as follows: A (right angle), B, and C.
- Draw a line segment BC and mark point D on BC such that AD is perpendicular to BC.
- Observe that triangles ABD and ACD are formed by the altitude AD.
- The angles in these triangles can be noted: ∠ADB=∠ABC (common angle), ∠ABD=∠ACD (both are right angles).
- Since both triangles share angle A and both have a right angle, by the AA (Angle-Angle) similarity criterion, we can conclude that △ABD∼△ACD.
- From the similarity of the triangles, we can write the proportion:
ABAC=BDDC
- Rearranging the proportion gives:
BD=ABAC⋅DC
- To find BDDC, we can rearrange the equation:
BDDC=ABAC
- The final result is:
BDDC=ABAC
The ratio BDDC is equal to ABAC.
Topper's Solved these Questions
- TRIANGLES BOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - TRIANGLES EXERCISE - Self Assessment Sheet
10 Videos
- TRIANGLES BOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - TRIANGLES EXERCISE - Self Assessment Sheet
10 Videos
- TIME AND WORK BOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - TIME AND WORK EXERCISE - Self Assessment Sheet - 20
10 Videos
- TRIGONOMETRICAL RATIOS BOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - TRIGONOMETRICAL RATIOS EXERCISE - Self Assessment Sheet - 40
1 Videos
Similar Questions
Knowledge Check
△ABC is a right angled at A and AD is the altitude to BC. If AB= 7 cm and AC = 24 cm. Find the ratio of AD is to AM if M is the mid-point of BC.
A25:41B32:41C336625D625336ΔABC is right angled at A and AB = 10 units .AC = 30 units and AD is perpendicular to BC. What is the area of ΔADB ?
A20B18C15D150
In the figure given below ABC is a triangle right angled at A and AC ⊥ BD . Show that
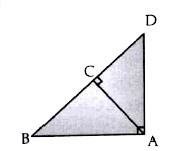
AD2=BD×DC
View SolutionIn the figure given below ABC is a triangle right angled at A and AC ⊥ BD . Show that

AB2=BC×BD
View SolutionIn the figure given below ABC is a triangle right angled at A and AC ⊥ CD . Show that
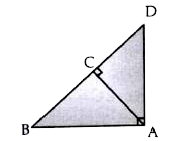
AC2=BC×DC
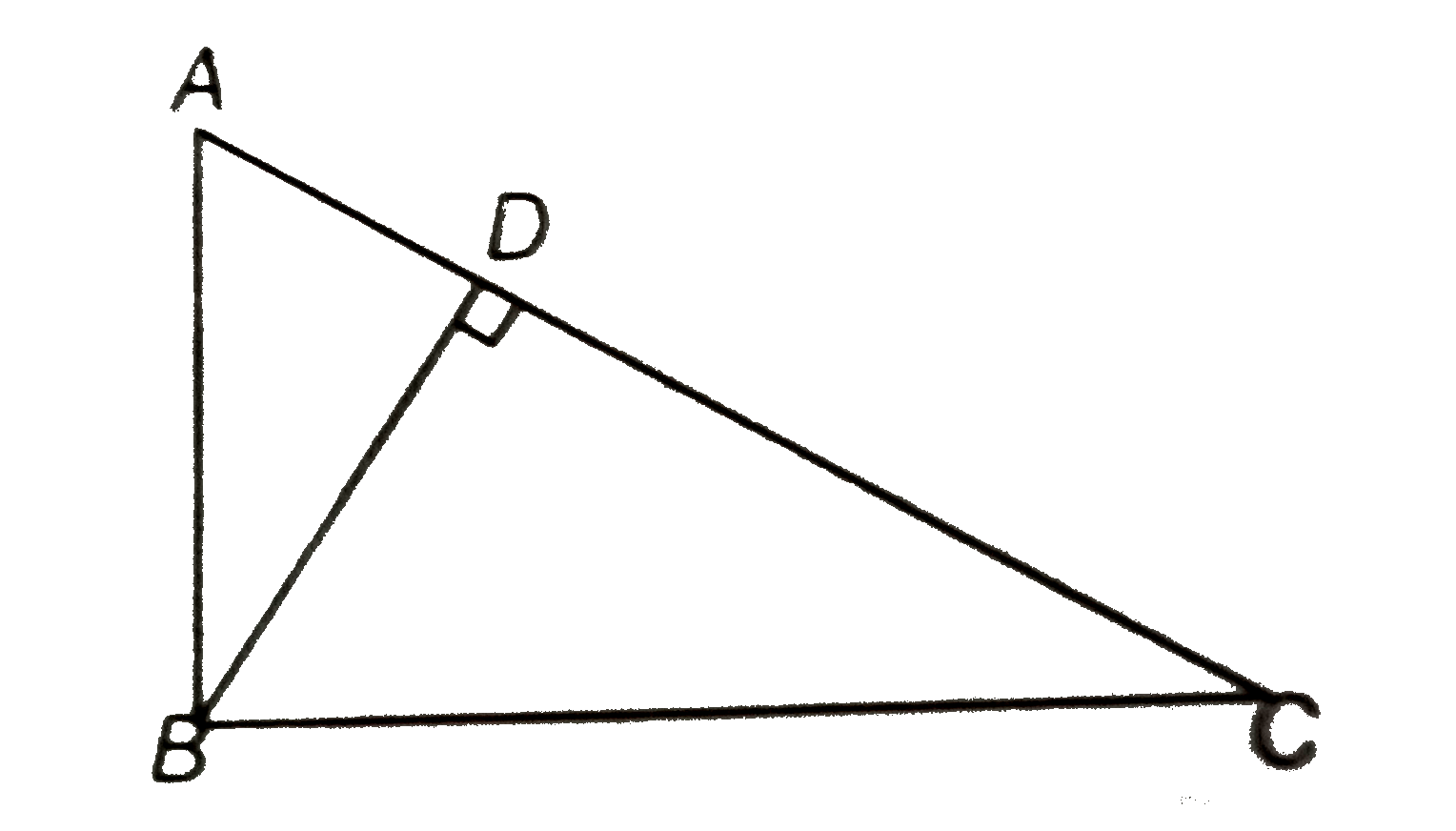
View SolutionIn given figure, ABC is a triangle right angled at B and BD⊥AC. If AD=4 cm and CD= 5 cm, then find BD and AB.
View SolutionIn the figure , ABD is a triangle right angled at A and AC ⊥ Bd . Show that

AD2=BD⋅CD
View SolutionΔABD is a right triangle, right-angled at A and AC⊥BD. Prove that AB2=BC×BD.
View Solution

