A circle is inscribed in an equilateral triangle of side a. What is the area of any square inscribed in the circle ?
a23
a24
a26
a28
The correct Answer is:C
To find the area of a square inscribed in a circle that is inscribed in an equilateral triangle with side length a, we can follow these steps:
Step 1: Find the radius of the inscribed circle (incircle) of the equilateral triangle.
The radius R of the incircle of an equilateral triangle can be calculated using the formula:
R=a2√3
where a is the length of a side of the triangle.
Step 2: Understand the relationship between the square and the circle.
When a square is inscribed in a circle, the diagonal of the square is equal to the diameter of the circle. Therefore, if the radius of the circle is R, the diameter D of the circle is:
D=2R
Step 3: Express the side length of the square in terms of the radius.
Let the side length of the square be s. The relationship between the side length s and the diagonal D of the square is given by:
D=s√2
Thus, we can express s as:
s=D√2=2R√2=R√2
Step 4: Substitute the radius into the side length formula.
Substituting the expression for R:
s=(a2√3)√2=a√22√3=a√66
Step 5: Calculate the area of the square.
The area A of the square is given by:
A=s2=(a√66)2=6a236=a26
Final Answer:
The area of the square inscribed in the circle is:
a26
The radius R of the incircle of an equilateral triangle can be calculated using the formula:
R=a2√3
where a is the length of a side of the triangle.
When a square is inscribed in a circle, the diagonal of the square is equal to the diameter of the circle. Therefore, if the radius of the circle is R, the diameter D of the circle is:
D=2R
Let the side length of the square be s. The relationship between the side length s and the diagonal D of the square is given by:
D=s√2
Thus, we can express s as:
s=D√2=2R√2=R√2
Substituting the expression for R:
s=(a2√3)√2=a√22√3=a√66
The area A of the square is given by:
A=s2=(a√66)2=6a236=a26
The area of the square inscribed in the circle is:
a26
Topper's Solved these Questions
- BOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - ALGEBRAIC EXPRESSIONS AND IDENTITIES EXERCISE - SELF ASSESSMENT SHEET10videos
ALGEBRAIC EXPRESSIONS AND IDENTITIES
- BOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - AREA AND PERIMETER OF RHOMBUS, TRAPEZIUM AND POLYGONS EXERCISE - Self Assessment Sheet-25 (Chapters 25 and 26)10videos
AREA AND PERIMETER OF RHOMBUS, TRAPEZIUM AND POLYGONS
Similar Questions
Knowledge Check
- Question 1 - Select One
A circle is cirumscribed in an equilateral triangle of side 'l'. The area of any square inscribed in the circle is :
A43l2B23l2C13l2Dl2 - Question 2 - Select One
A circle is inscribed in a equilateral triangle of side 24 cm. What is the area ( in cm2 ) of a square inscribed in the circle ?
A48B72C54D96 - Question 3 - Select One
The area of circle inscribed in an equilateral triangle of side 12 cm is
A12cm2Bπcm2C12πcm2DNone of these
A circle is inscribed in an equilateral triangle of side a. The area of any square inscribed in this circle is ______.
View SolutionA circle is inscribed in an equilateral triangle of side a. The area of any square inscribed in this circle is (A) a212 (B) a26 (C) a23 (D) 2a2
View SolutionWhat is the area of a square inscribed in a circle of diameter x cm?
View SolutionIn the given figure, a circle is inscribed in an equilateral triangle ABC of side 12 cm. Find the radius of inscribed circle and the area of the shaded region. [Use √3=1.73 and π=3.14]
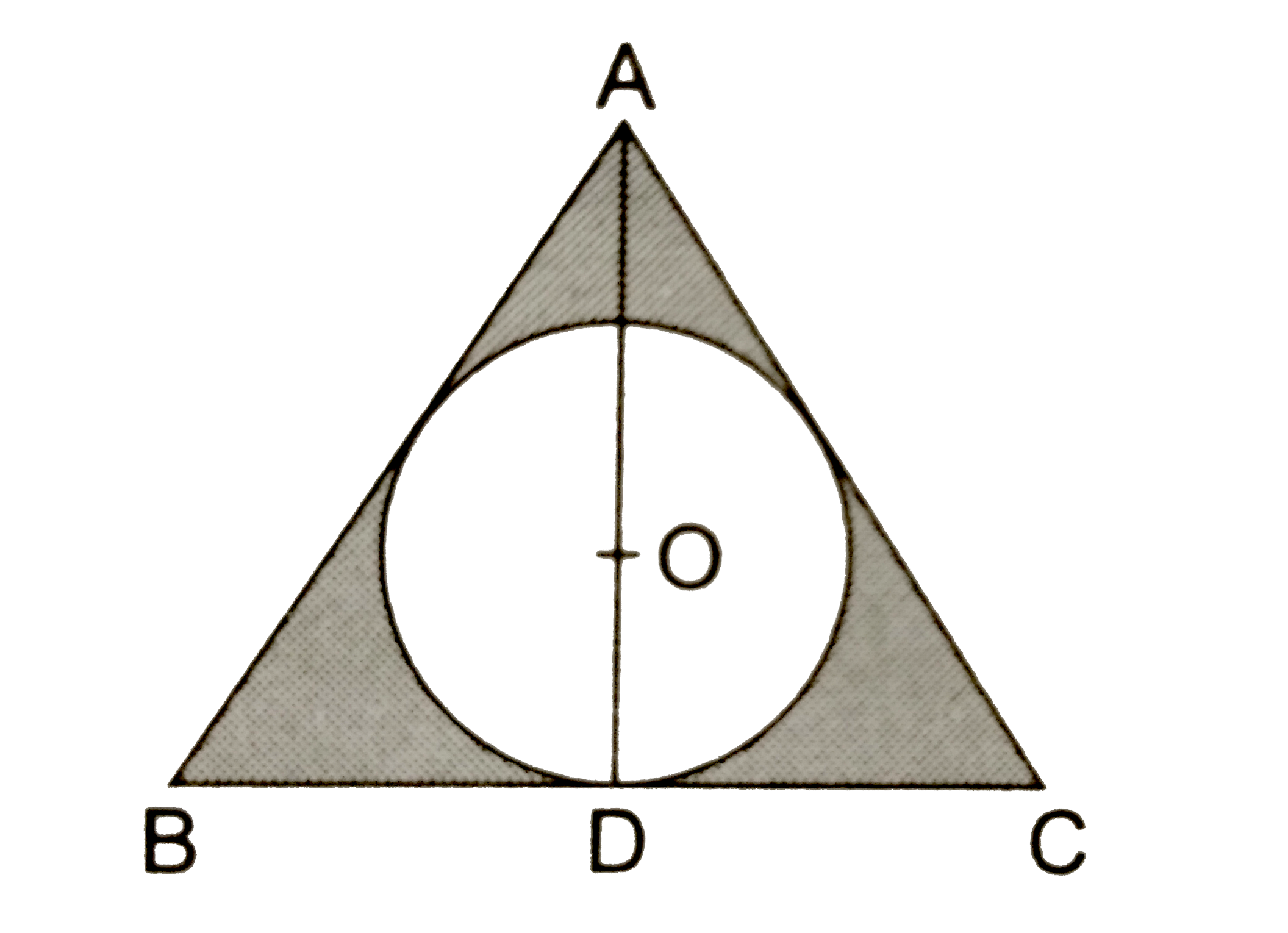 View Solution
View SolutionThe area of circle inscribed in an equilateral triangle of side 12 cm is
View Solution

