The perimeter of a rhombus is 40 cm. If the length of one of its diagonals be 12 m, then the length of the other diagonal is
14 cm
15 cm
16 cm
12 cm
The correct Answer is:C
To find the length of the other diagonal of a rhombus when given the perimeter and one diagonal, we can follow these steps:
1. Understand the properties of a rhombus: A rhombus has four equal sides and its diagonals bisect each other at right angles.
2. Given data:
- Perimeter (P) of the rhombus = 40 cm
- Length of one diagonal (d1) = 12 cm
3. Calculate the length of one side of the rhombus:
- The formula for the perimeter of a rhombus is:
P=4×side
- Rearranging this gives:
side=P4=40 cm4=10 cm
4. Determine the lengths of the diagonals:
- Let the length of the second diagonal be d2.
- Since the diagonals bisect each other at right angles, we can form two right triangles using half of each diagonal.
- Half of the first diagonal d1 is:
d12=12 cm2=6 cm
- Half of the second diagonal d2 is:
d22
5. Apply the Pythagorean theorem:
- In one of the right triangles formed, we have:
(half of d1)2+(half of d2)2=(side)2
- Substituting the known values:
62+(d22)2=102
- This simplifies to:
36+(d22)2=100
6. Solve for d22:
- Rearranging gives:
(d22)2=100−36=64
- Taking the square root:
d22=8
7. Calculate d2:
- Therefore, multiplying by 2 gives:
d2=2×8=16 cm
Final Answer:
The length of the other diagonal is 16 cm.
---
- Perimeter (P) of the rhombus = 40 cm
- Length of one diagonal (d1) = 12 cm
- The formula for the perimeter of a rhombus is:
P=4×side
- Rearranging this gives:
side=P4=40 cm4=10 cm
- Let the length of the second diagonal be d2.
- Since the diagonals bisect each other at right angles, we can form two right triangles using half of each diagonal.
- Half of the first diagonal d1 is:
d12=12 cm2=6 cm
- Half of the second diagonal d2 is:
d22
- In one of the right triangles formed, we have:
(half of d1)2+(half of d2)2=(side)2
- Substituting the known values:
62+(d22)2=102
- This simplifies to:
36+(d22)2=100
- Rearranging gives:
(d22)2=100−36=64
- Taking the square root:
d22=8
- Therefore, multiplying by 2 gives:
d2=2×8=16 cm
The length of the other diagonal is 16 cm.
Topper's Solved these Questions
- BOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - AREA AND PERIMETER OF RHOMBUS, TRAPEZIUM AND POLYGONS EXERCISE - Self Assessment Sheet-25 (Chapters 25 and 26)10videos
AREA AND PERIMETER OF RHOMBUS, TRAPEZIUM AND POLYGONS
- BOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - AREA AND PERIMETER OF RHOMBUS, TRAPEZIUM AND POLYGONS EXERCISE - Self Assessment Sheet-25 (Chapters 25 and 26)10videos
AREA AND PERIMETER OF RHOMBUS, TRAPEZIUM AND POLYGONS
- BOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - AREA AND PERIMETER OF RECTANGLE, SQUARE, PARALLELOGRAM, TRIANGLE AND CIRCLESEXERCISE - Question Bank - 25 (M.C.Q)15videos
AREA AND PERIMETER OF RECTANGLE, SQUARE, PARALLELOGRAM, TRIANGLE AND CIRCLES
- BOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - AVERAGEEXERCISE - SELF ASSESSMENT SHEET10videos
AVERAGE
Similar Questions
The perimeter of a rhombus is 40 cm. If the length of one of its diagonal is 10 cm, what is the length of the other diagonal?
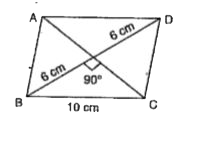 View Solution
View SolutionThe perimeter of a rhombus is 164 cm. If the length of one of the diagonals is 18 cm, find the length of ither diagonal. Hence, find the area of the rhombus
View Solution
Knowledge Check
- Question 1 - Select One
The perimeter of a rhombus is 20 cm. The length of one of its diagonal is 6 cm. What is the length of the other diagonal ?
A6 cmB9 cmC8 cmD10 cm - Question 2 - Select One
If the perimeter of a rhombus is 56 cm and the length of one of its diagonals is 26 cm. then find the length of the other diagonal of the rhombus.
A)6√7 cm
B)6√5 cm
C)6√3 cm
D)6√2 cmA6√7 cmB6√5 cmC6√3 cmD6√2 cm - Question 3 - Select One
The perimeter of a rhombus is 40 cm. If one of the diagonals be 12 cm long, what ia the length of the other diagonal ?
A12 cmB√136cmC16 cmD√44cm
The area of a rhombus is 150 cm2. The length of one of its diagonal is 10 cm. What is the length of the other diagonal ?
View SolutionThe area of a rhombus is 132 cm2. If length of one of its diagonals is 11 cm, then what is the length of the other diagonal?
View SolutionThe perimeter of a rhombus is 60 cm. If the length of its longer diagonal measures 24 cm, the length of the shorter diagonal is ........ cm.
View SolutionThe area of a rhombus is 150cm2. The length of one of its diagonals is 10 cm. The length of the other diagonal is :
View SolutionThe area of a rhombus is 36 cm and the length of one of its diagonals is 6 cm. The length of the second diagonal is
View Solution

