Seven of the eight numbers in a distribution are 11, 16, 6, 10, 13, 11, 13
Given that the median of the distribution is 12, find the mean of the distribution.
12
11
The correct Answer is:C
To solve the problem step-by-step, we will follow the reasoning laid out in the video transcript.
Step 1: Identify the given numbers and the unknown
We are given seven numbers: 11, 16, 6, 10, 13, 11, and 13. We need to find the eighth number, which we will denote as x.
Step 2: Arrange the numbers in ascending order
To find the median, we need to arrange the numbers in ascending order. Including x, the numbers will be:
- 6, 10, 11, 11, x, 13, 13, 16
Step 3: Understand the median condition
We know that the median of the distribution is 12. Since there are 8 numbers, the median will be the average of the 4th and 5th numbers in the ordered list.
Step 4: Set up the equation for the median
The 4th and 5th numbers in the ordered list are:
- 4th number: 11
- 5th number: x
According to the median formula:
Median=4th number+5th number2=12
Substituting the known values:
11+x2=12
Step 5: Solve for x
Multiply both sides by 2 to eliminate the fraction:
11+x=24
Now, subtract 11 from both sides:
x=24−11=13
Step 6: List all the numbers including x
Now that we have found x=13, the complete list of numbers is:
- 6, 10, 11, 11, 13, 13, 13, 16
Step 7: Calculate the mean
To find the mean, we sum all the numbers and divide by the total number of observations (which is 8):
Mean=6+10+11+11+13+13+13+168
Step 8: Perform the addition
Calculating the sum:
6+10+11+11+13+13+13+16=93
Step 9: Divide by the number of observations
Now divide the sum by 8:
Mean=938=11.625
Final Answer
The mean of the distribution is 11.625.
---
We are given seven numbers: 11, 16, 6, 10, 13, 11, and 13. We need to find the eighth number, which we will denote as x.
To find the median, we need to arrange the numbers in ascending order. Including x, the numbers will be:
- 6, 10, 11, 11, x, 13, 13, 16
We know that the median of the distribution is 12. Since there are 8 numbers, the median will be the average of the 4th and 5th numbers in the ordered list.
The 4th and 5th numbers in the ordered list are:
- 4th number: 11
- 5th number: x
Median=4th number+5th number2=12
Substituting the known values:
11+x2=12
Multiply both sides by 2 to eliminate the fraction:
11+x=24
Now, subtract 11 from both sides:
x=24−11=13
Now that we have found x=13, the complete list of numbers is:
- 6, 10, 11, 11, 13, 13, 13, 16
To find the mean, we sum all the numbers and divide by the total number of observations (which is 8):
Mean=6+10+11+11+13+13+13+168
Calculating the sum:
6+10+11+11+13+13+13+16=93
Now divide the sum by 8:
Mean=938=11.625
The mean of the distribution is 11.625.
Topper's Solved these Questions
- BOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - DATA HANDLING EXERCISE - Self Assessment Sheet - 2710videos
DATA HANDLING
- BOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - COMPOUND INTEREST EXERCISE - Self Assessment Sheet - 1910videos
COMPOUND INTEREST
- BOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - DISTANCE, TIME AND SPEED EXERCISE - Unit Test-320videos
DISTANCE, TIME AND SPEED
Similar Questions
Knowledge Check
- Question 1 - Select One
Find the median of the distribution. 5, 9, 4, 6, 12, 8
A7B9C6D5 - Question 2 - Select One
If the mean of the following distribution is 6, then find the value of a.
 A6B7C4D3
A6B7C4D3 - Question 3 - Select One
If the standard deviation of the binomial distribution (q+p)16 is 2, then mean of the distribution is
A6B8C10D12
Find the median of the following distribution
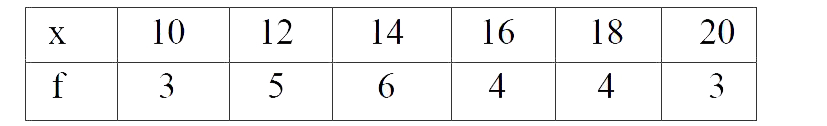 View Solution
View SolutionFind the median of the following distribution
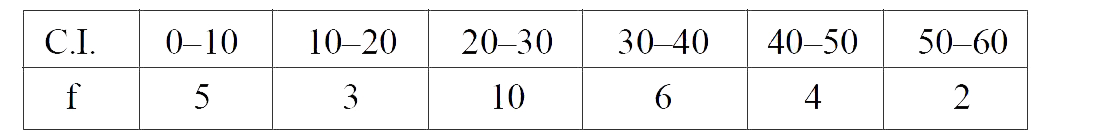 View Solution
View SolutionIf mean of the given distribution is 65.6 find the missing frequency.
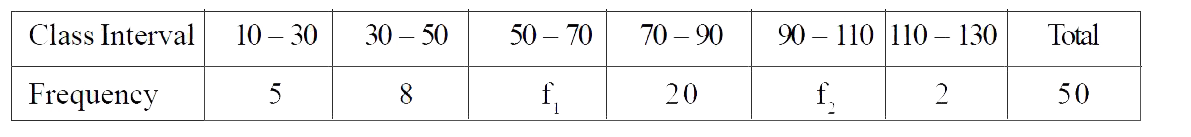 View Solution
View SolutionFind the median for the following distribution :
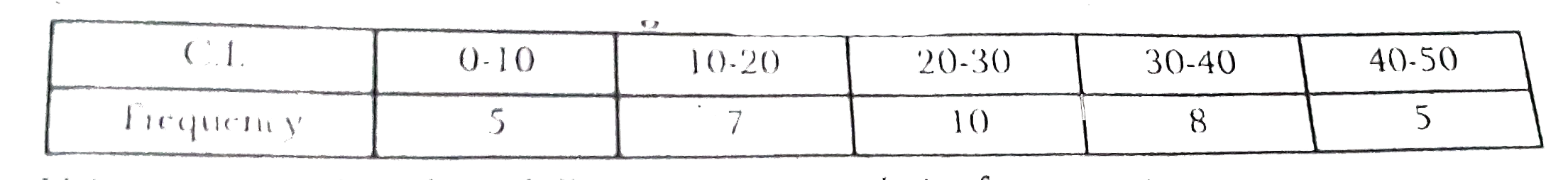 View Solution
View SolutionFor the given frequency distribution find the median.
 View Solution
View Solution

