Calculate the water pressure and the thrust at the bottom of a tank whose length width and the depth are 2m, 1.5 m and 1m respectively. Density of water is 1000kgm−3
To solve the problem of calculating the water pressure and the thrust at the bottom of a tank, we can follow these steps:
Step 1: Calculate the Pressure at the Bottom of the Tank
The formula for pressure (P) at a certain depth in a fluid is given by:
P=ρ⋅g⋅h
where:
- ρ = density of the fluid (water in this case) = 1000kg/m3
- g = acceleration due to gravity = 9.8m/s2
- h = depth of the fluid = 1m
Substituting the values into the formula:
P=1000kg/m3⋅9.8m/s2⋅1m
P=9800N/m2
Step 2: Calculate the Area of the Bottom of the Tank
The area (A) of the bottom of the tank can be calculated using the formula:
A=length⋅width
Given:
- Length = 2m
- Width = 1.5m
Calculating the area:
A=2m⋅1.5m
A=3m2
Step 3: Calculate the Thrust at the Bottom of the Tank
The thrust (F) exerted at the bottom of the tank can be calculated using the formula:
F=P⋅A
Substituting the values we found:
F=9800N/m2⋅3m2
F=29400N
Final Answers
- The water pressure at the bottom of the tank is 9800N/m2.
- The thrust at the bottom of the tank is 29400N.
---
The formula for pressure (P) at a certain depth in a fluid is given by:
P=ρ⋅g⋅h
where:
- ρ = density of the fluid (water in this case) = 1000kg/m3
- g = acceleration due to gravity = 9.8m/s2
- h = depth of the fluid = 1m
P=1000kg/m3⋅9.8m/s2⋅1m
P=9800N/m2
The area (A) of the bottom of the tank can be calculated using the formula:
A=length⋅width
Given:
- Length = 2m
- Width = 1.5m
A=2m⋅1.5m
A=3m2
The thrust (F) exerted at the bottom of the tank can be calculated using the formula:
F=P⋅A
Substituting the values we found:
F=9800N/m2⋅3m2
F=29400N
- The water pressure at the bottom of the tank is 9800N/m2.
- The thrust at the bottom of the tank is 29400N.
Similar Questions
Calculate the water pressure and the thrust at the bottom of a tank whose length width and the depth are 2m, 1.5 m and 1m respectively. Density of water is 1000kgm−3
View SolutionCalculate the mass of air enclosed in a room of length, breadth and height equal to 5m, 3m and 4m respectively. Density of air =1.3kgm3.
View Solution
Knowledge Check
The capacity of a cuboid tank of water is 50000 L. Find the breadth of the tank, if its length and depth are 2.5 m and 10 m, respectively.
A2mB4 mC9 mD6 mA block of wood floats with 1//4 of its volume under water. What is he density of wood? (Density of water =1000kg/m3)
A750kg/m3B250kg/m3C300kg/m3D260kg/m3The time taken by the sunlight to reach the bottom of a tank of depth 4.5 m filled completely with water is …………. Ns. The refractive index of water is 43.
A2B20C1.5D200
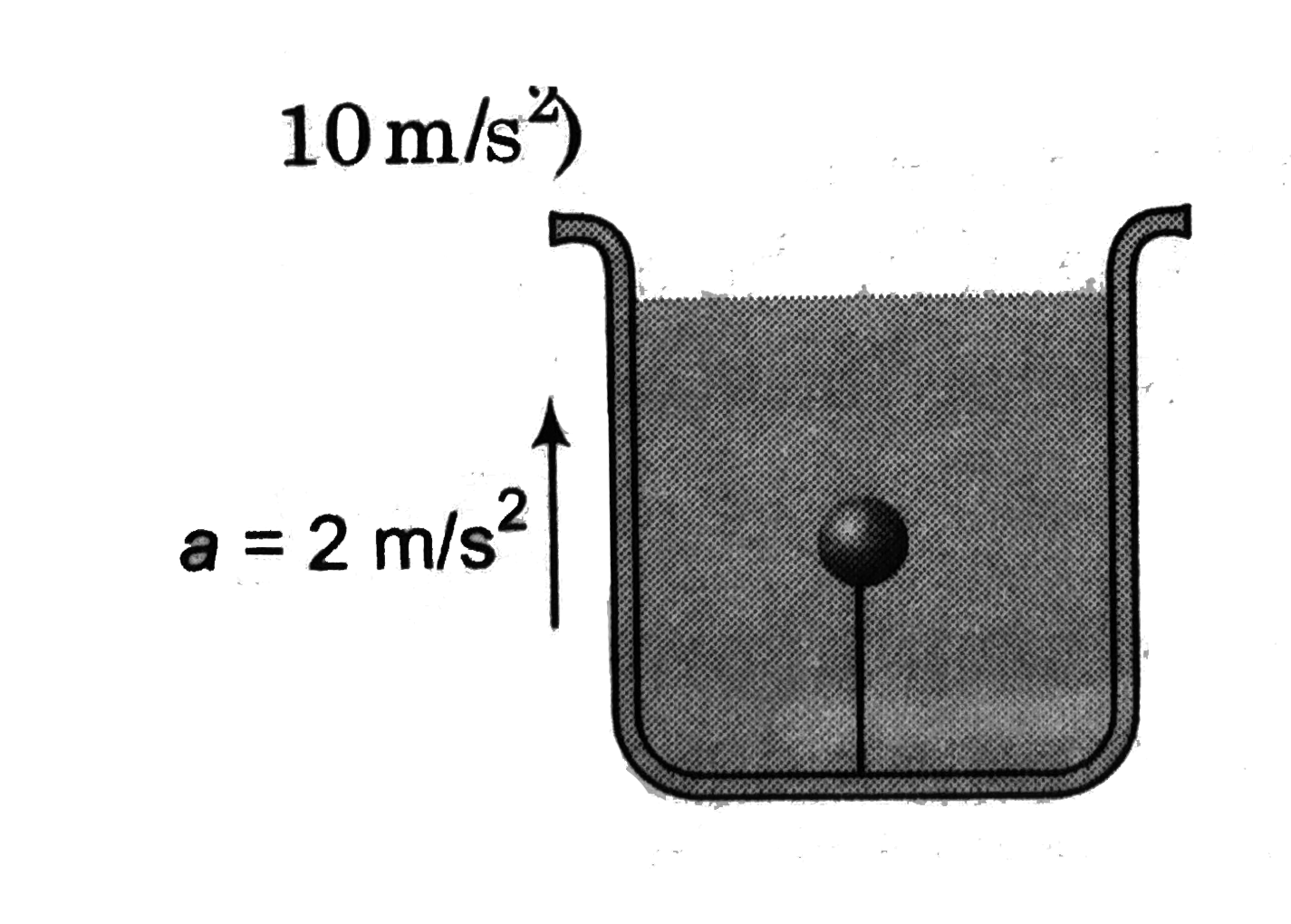
A solid sphere of mass m=2kg and specific gravity s=0.5 is held stationary relative to a tank filled with water. The tank is accelerating upward with acceleration 2m/s2. Calculate
(a) Tension in the thread connected between the sphere and the bottom of the tank.
(b) If the thread snaps, calculate the acceleration of sphere with respect to the tank.
(Density of water =1000kgm−3,g=10ms−2).
 .
.
View SolutionA solid sphere of mass m=2kg and density ρ=500kg/m3 is held stationary relative to a tank filled with water. The tank is acceerating upward with acceleration 2m/s2. Calculate
(a) Tension in the thread connected between the sphere and the bottom of the tank.
(b) If the thread snaps, calculate the acceleration of sphere with respect to the tank. (Density of water=1000kg/m3,g=10m/s2)
View SolutionA canal lock gate is 4 m broad and the depth of water on opposite side of the gate are 5m and 2m . Find the resultant thrust on the gate and the torque tending to ture the gate about its base. Density of water =1000kgm−3andg=9.8ms−2
View SolutionCalculate the molarity of water if its density is 1000kgm−3
View SolutionCalculate the total pressure at the bottom of a lake of depth 5.1 m (atm pressure =105 P), density of water =103kg/m3,g=10m/s2
View Solution
