A tiny planet like rocky bodies that orbit the sun ______.
Step-by-Step Solution:
1. Understanding the Question: The question asks for a specific term that describes tiny, planet-like rocky bodies that orbit the sun.
2. Identifying Solar System Bodies: In our solar system, there are several types of celestial bodies that orbit the sun. The most common are planets, moons, comets, and asteroids.
3. Analyzing the Characteristics:
- Planets: These are large bodies that orbit the sun. They can be rocky (like Earth) or gas giants (like Jupiter), but they are not tiny.
- Moons: These are natural satellites that orbit planets, not the sun directly.
- Comets: These are made of ice and dust and have a long tail when they come close to the sun, but they are not typically described as rocky.
- Asteroids: These are small, rocky bodies that orbit the sun, fitting the description of being tiny and rocky.
4. Conclusion: Based on the analysis, the correct term for tiny, planet-like rocky bodies that orbit the sun is "asteroids." Additionally, there is a specific region in the solar system known as the asteroid belt, located between Mars and Jupiter, where many of these asteroids are found.
5. Final Answer: A tiny planet-like rocky bodies that orbit the sun are called asteroids.
---
- Planets: These are large bodies that orbit the sun. They can be rocky (like Earth) or gas giants (like Jupiter), but they are not tiny.
- Moons: These are natural satellites that orbit planets, not the sun directly.
- Comets: These are made of ice and dust and have a long tail when they come close to the sun, but they are not typically described as rocky.
- Asteroids: These are small, rocky bodies that orbit the sun, fitting the description of being tiny and rocky.
Similar Questions
Knowledge Check
A planet of mass m is the elliptical orbit about the sun (m<<Msun) with an orbital period T. If A be the area of orbit, then its angular momentum would be:
A2mATBmATCmA2TD2mATFor motiion of planets in ellipticla orbits around the sun the central force is
Athe force on the plantet along the vector joining the sun and the planetBthe force on the sun along the vector joining the sun and the other focus of the ellipseCthe force on the planet along the line joining focus of the ellipseDnone of the aboveA planet is revolving in an elliptical orbit around the sun. Its closest distance from the sun is r and the farthest distance is R. If the velocity of the planet nearest to the sun be v and that farthest away from the sun be V. then v/V is
AR2/r2Br2/R2CR/rDr/R
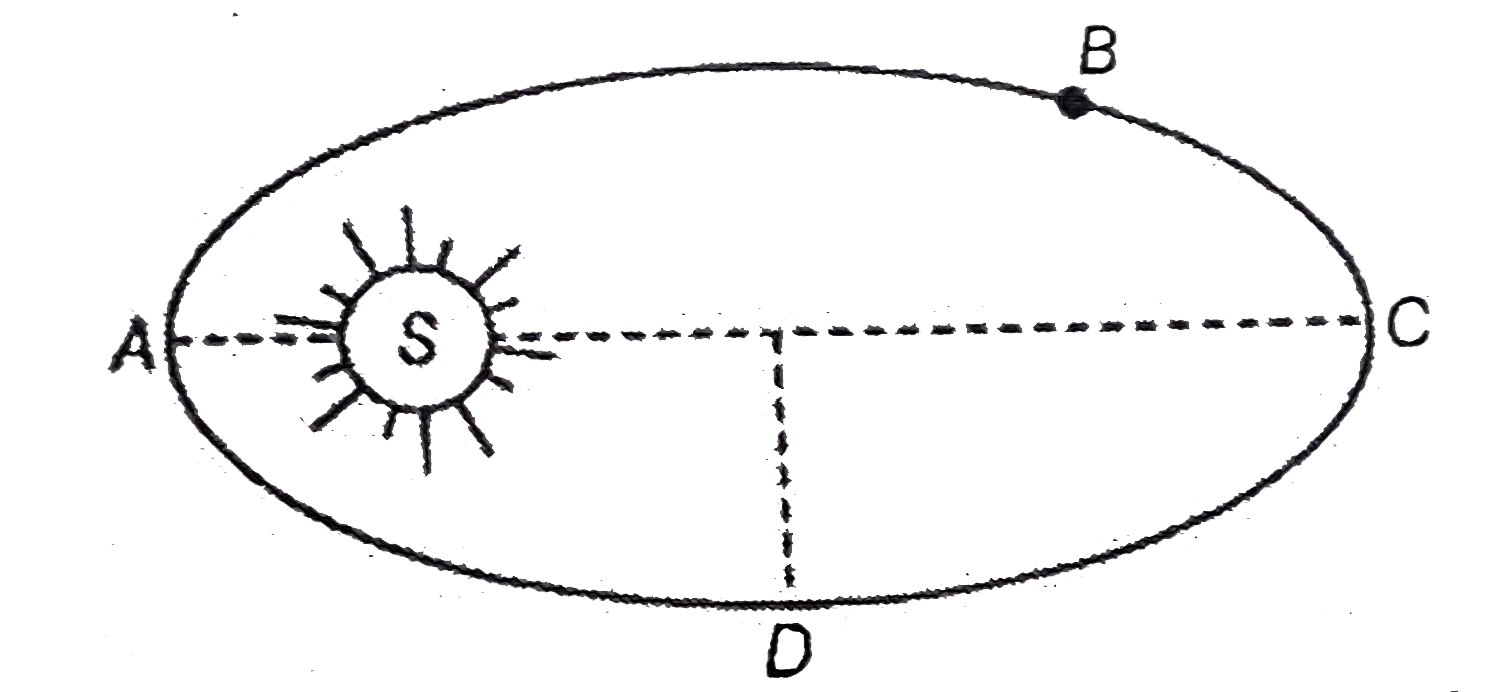
A planet revolves in elliptical orbit around the sun. (see figure). The linear speed of the planet will be maximum at
View SolutionIf a and b are the nearest and farthest distances of a planet from the sun and the planet is revolving in an elliptical orbit, then square of the time period of revolution of that planets is directly proportional to
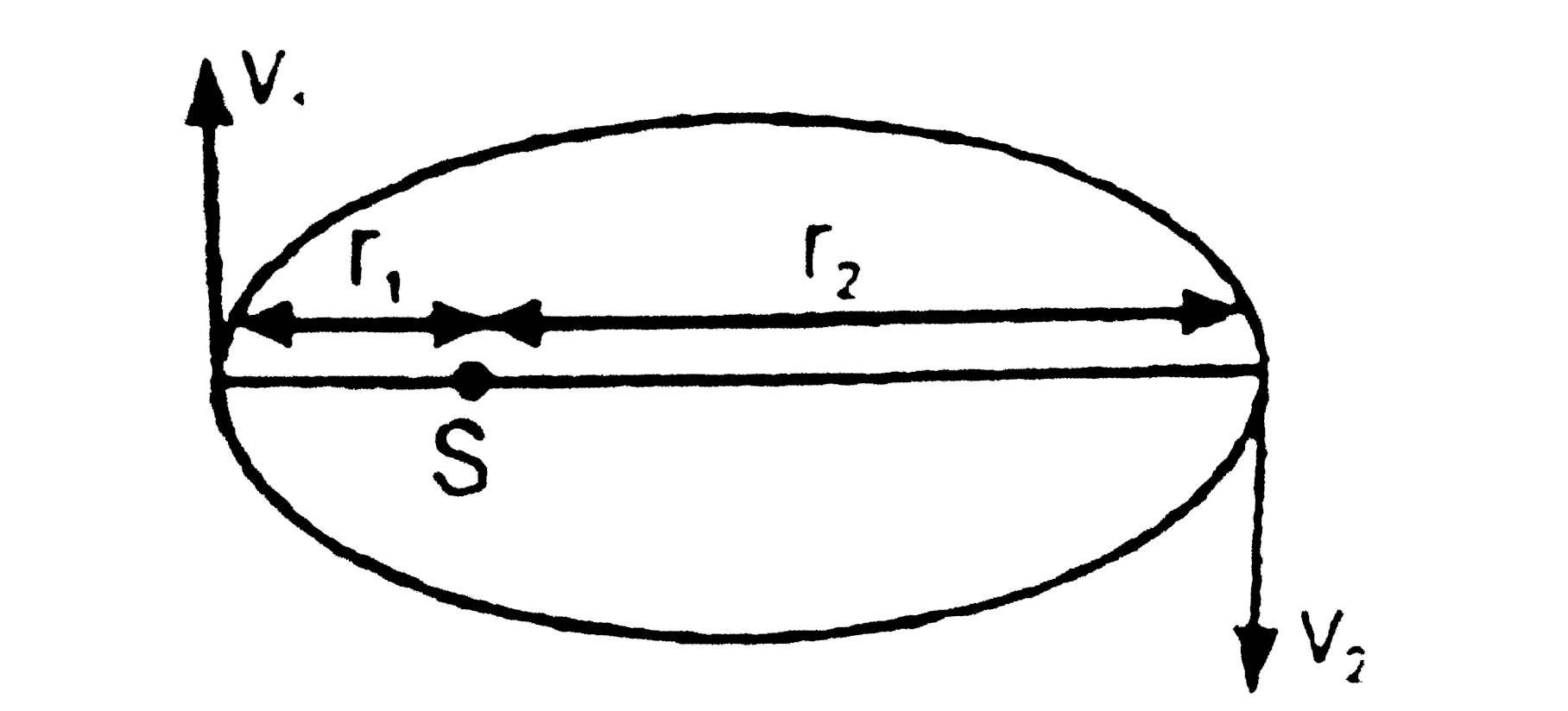
View SolutionA planet is revolving in an elliptical orbit around the sun as shown in the figure. The areal velocity (area swapped by the radius vector with respect to sun in unit time) is:
View SolutionIn the solar system, apart from the star, planets and satellites, there are numerous tiny bodies which also move around the sun. These bodies are called asteroids. They are found
View SolutionAll planets move in elliptical orbits with the sun situtated at one of the forci of the ellipse the point at wihich the planet is closest to the sun is
View Solution

