Draw any angle with vertex O Take a point A on one of its arms and B on another such that OA = OB. Draw the perpendicular bisectors of $¯ ¯¯¯¯ ¯ O A$ and $¯ ¯¯¯¯ ¯ O B .$ Let them meet at P. Is PA = PB ?

Video Solution

|

Answer

Step by step video & image solution for Draw any angle with vertex O Take a point A on one of its arms and B on another such that OA = OB. Draw the perpendicular bisectors of bar(OA) and bar(OB). Let them meet at P. Is PA = PB ? by Maths experts to help you in doubts & scoring excellent marks in Class 6 exams.

Updated on:21/07/2023

Class 6 MATHS PRACTICAL GEOMETRY

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A variable line is drawn through the origin O. Two points A and B same side of O are taken on the line such that $O A = 1$ and $O B = 2$ unit. . Through points A and B two lines are drawn making equal angle $α$ with the line AB. Then the locus of the point of intersection of the lines, is:
A $x^{2} + y^{2} = \frac{9 + {tan}^{2} α}{4}$
B $x^{2} + y^{2} = \frac{9 - {tan}^{2} α}{4}$
C $x^{2} + y^{2} = \frac{9 + {tan}^{2} α}{2}$
D $x^{2} + y^{2} = \frac{9 + 2 {tan}^{2} α}{4}$
Question 2 - Select One
On the circle with centre O, points A, B are such that OA =AB. A point C is located on the tangent at B to the circle such that A and C are on the opposite sides of the line OB and Ab =BC. The line segment AC intersects the circle again at F. Then the ratio $∠ B O F : ∠ B O C$ is equal to-

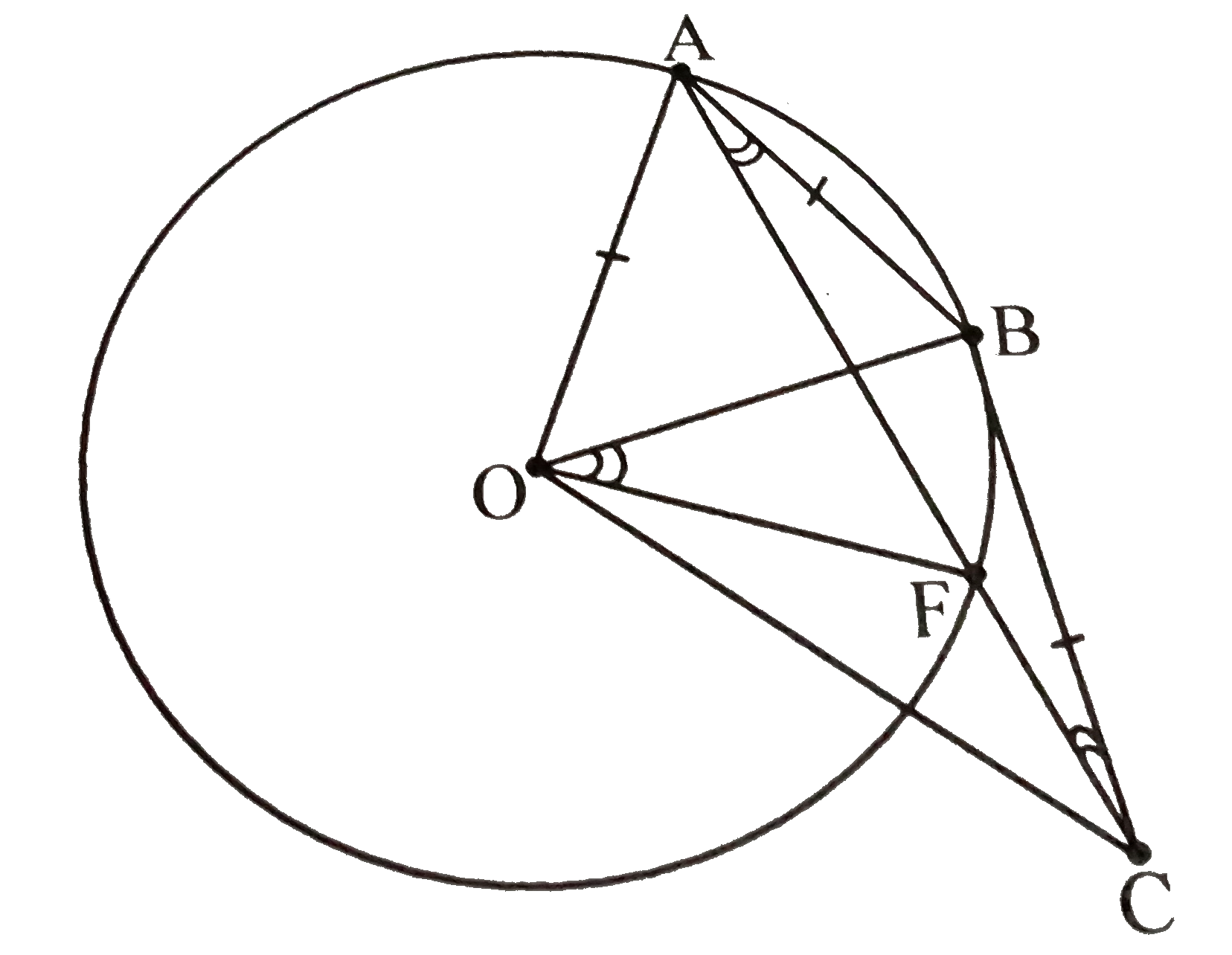A $1 : 2$
B $2 : 3$
C $3 : 4$
D $4 : 5$
Question 3 - Select One
Let $O$ , $A$ , $B$ be three collinear points such that $O A . O B = 1$ . If $O$ and $B$ represent the complex numbers $O$ and $z$ , then $A$ represents
A $\frac{1}{¯ z}$
B $\frac{1}{z}$
C $¯ z$
D $z^{2}$

MTG IIT JEE FOUNDATION-PRACTICAL GEOMETRY -NCERT SECTION (EXERCISE 14.5)

Home
Ask Doubt
Profile