Passage I: Given condition are : AB=6cm, BC=7cm, CD=3cm, AD=5.5cm and AC=11cm.
Is it possible to construct a quadrilateral?
No, since in ΔACD,AD+CD<AC
yes
Data is insufficient
None of these
To determine whether it is possible to construct a quadrilateral with the given sides, we will use the triangle inequality theorem. This theorem states that the sum of the lengths of any two sides of a triangle must be greater than the length of the third side. For a quadrilateral, we can apply this principle to the sides.
1. Identify the sides of the quadrilateral:
- Let the sides be:
- AB = 6 cm
- BC = 7 cm
- CD = 3 cm
- AD = 5.5 cm
- AC = 11 cm
2. Check the triangle inequalities:
- For a quadrilateral to be formed, the sum of the lengths of any three sides must be greater than the length of the fourth side. We will check the following combinations:
a. Check AB + BC + CD > AD:
- 6 cm + 7 cm + 3 cm = 16 cm > 5.5 cm (True)
b. Check AB + BC + AD > CD:
- 6 cm + 7 cm + 5.5 cm = 18.5 cm > 3 cm (True)
c. Check AB + AD + CD > BC:
- 6 cm + 5.5 cm + 3 cm = 14.5 cm > 7 cm (True)
d. Check BC + AD + CD > AB:
- 7 cm + 5.5 cm + 3 cm = 15.5 cm > 6 cm (True)
e. Check AB + AC > BC:
- 6 cm + 11 cm = 17 cm > 7 cm (True)
f. Check AC + AD > CD:
- 11 cm + 5.5 cm = 16.5 cm > 3 cm (True)
g. Check AC + BC > AB:
- 11 cm + 7 cm = 18 cm > 6 cm (True)
3. Conclusion:
- Since all the inequalities hold true, it is possible to construct a quadrilateral with the given sides.
Final Answer:
Yes, it is possible to construct a quadrilateral with the given sides.
- Let the sides be:
- AB = 6 cm
- BC = 7 cm
- CD = 3 cm
- AD = 5.5 cm
- AC = 11 cm
- For a quadrilateral to be formed, the sum of the lengths of any three sides must be greater than the length of the fourth side. We will check the following combinations:
a. Check AB + BC + CD > AD:
- 6 cm + 7 cm + 3 cm = 16 cm > 5.5 cm (True)
b. Check AB + BC + AD > CD:
- 6 cm + 7 cm + 5.5 cm = 18.5 cm > 3 cm (True)
c. Check AB + AD + CD > BC:
- 6 cm + 5.5 cm + 3 cm = 14.5 cm > 7 cm (True)
d. Check BC + AD + CD > AB:
- 7 cm + 5.5 cm + 3 cm = 15.5 cm > 6 cm (True)
e. Check AB + AC > BC:
- 6 cm + 11 cm = 17 cm > 7 cm (True)
f. Check AC + AD > CD:
- 11 cm + 5.5 cm = 16.5 cm > 3 cm (True)
g. Check AC + BC > AB:
- 11 cm + 7 cm = 18 cm > 6 cm (True)
- Since all the inequalities hold true, it is possible to construct a quadrilateral with the given sides.
Yes, it is possible to construct a quadrilateral with the given sides.
Topper's Solved these Questions
- PRACTICAL GEOMETRYBOOK - MTG IIT JEE FOUNDATIONCHAPTER - PRACTICAL GEOMETRYEXERCISE - EXERCISE (SUBJECTIVE PROBLEMS LEVEL-2)
33 Videos
- PRACTICAL GEOMETRYBOOK - MTG IIT JEE FOUNDATIONCHAPTER - PRACTICAL GEOMETRYEXERCISE - EXERCISE (MULTIPLE CHOICE QUESTIONS LEVEL-2)
8 Videos
- PLAYING WITH NUMBERSBOOK - MTG IIT JEE FOUNDATIONCHAPTER - PLAYING WITH NUMBERSEXERCISE - Olympiad/HOTS Corner
6 Videos
- RATIONAL NUMBERS BOOK - MTG IIT JEE FOUNDATIONCHAPTER - RATIONAL NUMBERS EXERCISE - Olympiad/HOTS Corner
20 Videos
Similar Questions
Given AB=3cm, BC=5cm, AC=9cm, AD=6cm, CD=2cm. Which of the following is true about the construction of a quadrilateral?
View SolutionIn a quadrilateral ABCD,AB=5cm,BC=37cm,CD=35cm,BD=12cm and AD=13cm . Find its area
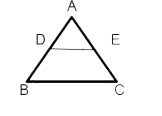
View SolutionIn the given figure, AD = 2cm, BD = 3 cm, AE = 3.5 cm and AC = 7 cm. Is DE parallel to BC ?
View SolutionConstruct a quadrilateral ABCD in which AB=3.8cm, BC=5cm,CD=5cm, DA=5.5cm and AC=8cm.
View SolutionConstruct a kite ABCD in which AB=4cm, AD=6cm and AC=6cm.
View SolutionConstruct a quadrilateral ABCD with AB=3 cm, AB=3cm, AD=2.7 cm, DB=3.6 cm, ∠B=110∘ and BC=4.2 cm. Construct another quadrilateral A'BC'D' similar to quadrilateral ABCD so that diagonal BD'=4.8 cm.
View SolutionFind the area of a quadrilateral ABCD in which AB=3 cm, BC=4 cm, CD=4 cm, DA=5 cm and AC=5 cm.
View SolutionFind the area of the quadrilateral ABCD in which AB=3cm,BC=4cm,CD=4cm,DA=5cm and AC=5cm.
View SolutionIn a quadrilateral ABCD , AB = 5 cm , BC = 37 cm , CD = 35 cm , BD = 12 cm , and AD = 13 cm . Find its area .
View SolutionConstruct a quadrilateral when AB=5.5cm, BC=4.4.cm, AD=3.3cm, CD=4.6cm and BD=6.6cm.
View Solution
