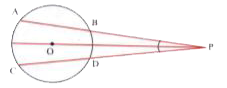
If OP is the angular bisector of angle BPD an O is the centre, then which of the following is correct?

A

AB = CD

B

$A B > C D$

C

$A B < C D$

D

$A B + C D = 2 O P$

Text Solution

Verified by Experts

The correct Answer is:A

|

Updated on:21/07/2023

Class 9 MATHS CIRCLES

Topper's Solved these Questions

BOOK - CENGAGECHAPTER - CIRCLESEXERCISE - OLYMPIAD AND NTSE LEVEL EXERCISES
6videos
CIRCLES
BOOK - CENGAGECHAPTER - CIRCLESEXERCISE - TEST YOURSELF (LEVEL 3)
8videos
CIRCLES
BOOK - CENGAGECHAPTER - ALGEBRAIC EXPRESSIONS AND POLYNOMIALS EXERCISE - OLYMPIAD AND NTSE LEVEL EXERCISES
10videos
ALGEBRAIC EXPRESSIONS AND POLYNOMIALS
BOOK - CENGAGECHAPTER - LAWS OF EXPONENTS AND LOGARITHMS EXERCISE - OLYMPIAD AND NTSE LEVEL EXERCISES
10videos
LAWS OF EXPONENTS AND LOGARITHMS

Similar Questions

Knowledge Check

Question 1 - Select One
In the given figure, PQRS is a parallelogram and $∠ S P Q = 60^{\circ}$ . If the bisectors of $∠ P and ∠ Q$ meet at A on RS, then which of the following is not correct ?

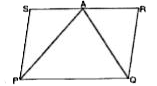AAS = SP
BAS = AR
CAR = SP
DAQ = PQ
Question 2 - Select One
In a $Δ A B C$ , if the bisector of the angle BAC meets BC in D, then which one of the following is correct?
A $A B \leq B D$
B $∠ D B A > \frac{1}{2} ∠ B A C$
C $Δ A B D$ can never be isosceles
DIf $B D = A D$ , then $Δ A B D$ will be equilateral.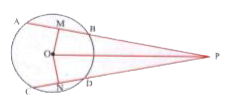
Question 3 - Select One

If OM = ON and $∠ O M P = ∠ O N P = 90^{\circ}$ , where O is the centre, then which of following is correct?
A $∠ O P M > ∠ O P N$
B $∠ O P M < ∠ O P N$
C $∠ O P M = ∠ O P N$
D $∠ O P M + ∠ O P N = 270^{\circ}$

CENGAGE-CIRCLES-TEST YOURSELF (MULTIPLE CHOICE QUESTION)

Home
Ask Doubt
Profile