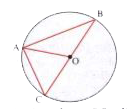
In the above figure, BC is diameter and O is centre. If area (ΔOAB)=k× area (ΔOAC) then K is
A
√2
B
12
C
1
D
2
Text Solution
The correct Answer is:C
|
Topper's Solved these Questions
- CIRCLESBOOK - CENGAGECHAPTER - CIRCLESEXERCISE - OLYMPIAD AND NTSE LEVEL EXERCISES
6 Videos
- CIRCLESBOOK - CENGAGECHAPTER - CIRCLESEXERCISE - TEST YOURSELF (LEVEL 3)
8 Videos
- ALGEBRAIC EXPRESSIONS AND POLYNOMIALS BOOK - CENGAGECHAPTER - ALGEBRAIC EXPRESSIONS AND POLYNOMIALS EXERCISE - OLYMPIAD AND NTSE LEVEL EXERCISES
10 Videos
- LAWS OF EXPONENTS AND LOGARITHMS BOOK - CENGAGECHAPTER - LAWS OF EXPONENTS AND LOGARITHMS EXERCISE - OLYMPIAD AND NTSE LEVEL EXERCISES
10 Videos
Similar Questions
Knowledge Check
In the given figure, l∣∣BC and D is the mid-point of BC. If area (ΔABC) = a x area(ΔEDC), then find the value of a.
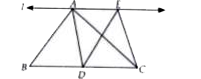 A1B2C3D4
A1B2C3D4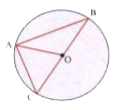
In the above figure, O is the centre and BC = 6 cm. If ∠OBA=45∘, then area (ΔOAB) isA18cm2B4cm2C9cm2D4.5cm2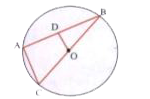
In the above diagram, BC is diameter, O is centre and OD⊥AB. If AC=λOD, then value of λ isA2B3C1D12
In the figure, AB is a diameter of the circle with centre O and OA = 7cm. Find the area of the shaded region
View SolutionIn the figure, AB is a diameter of the circle with centre O and OA = 7cm. Find the area of the shaded region
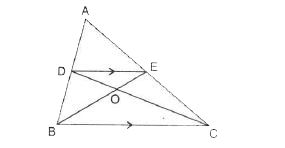
View SolutionIn the following figure, DE is parallel to BC. Show that :
(i) Area(ΔADC)=Area(ΔAEB)
(ii) Area(ΔBOD)=Area(ΔCOE).
View Solution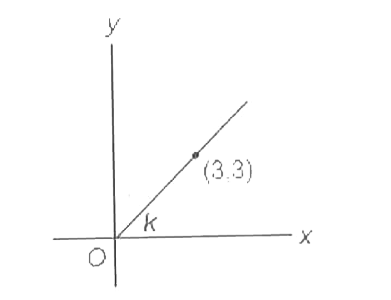
In the figure above, sink=?
View Solution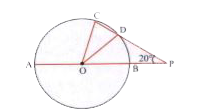
In the above figure, AB is diameter with length 2x. If ∠APC=20∘andOD=DP, where O is the centre, then length of AC is
View Solution

