N identical cells, each of emf E and internal resistance r are joined in series. Out of N cells, n cells are wrongly connected i.e., their terminals are connected in reverse of that required for series connection. (n<N2). Let E0 be the emf of resulting battery and r0 be its internal resistance. then
E0=(N−n)E,r0=(N−n)r
E0=(N−2n)E,r0=(N−2n)r
E0=(N−2n)E,r0=Nr
E0=(N−n)E,r0=Nr
The correct Answer is:C
For every cell that is wrongly connected, the emf decreases by 2E. However, internal resistance does not depend on the direction and therefore remains same for all cells.
Topper's Solved these Questions
- SOURCES OF ELECTRIC CURRENTBook:CENGAGE PHYSICSChapter:SOURCES OF ELECTRIC CURRENTExercise:CHALLENGING EXERCISE
Explore 10 Videos
- REFRACTION OF LIGHT Book:CENGAGE PHYSICSChapter:REFRACTION OF LIGHT Exercise:OLYMPIAD AND NSE LEVEL EXCERCISES
Explore 10 Videos
- STATIC ELECTRICITYBook:CENGAGE PHYSICSChapter:STATIC ELECTRICITYExercise:OLYMPIAD AND NTSE LEVEL EXERCISES
Explore 10 Videos
Similar Questions
N identical cells, each of emf ε and internal resistances r are joined in series. Out of these, n cells are wrongly connected, i.e. their terminals are connected in reverse order as required for series connection. If εo be the emf of the resulting battery and ro be its internal resistance then for n <N/2
View Solutionn-identical cells each of emf E and internal resistance r are connected in series. Find the expression for current in the circuit given below

View Solution
Knowledge Check
N identical cells, each emf E and internal resistance r are joined in series. Out of N cells, n cells are wrongly connected i.e., their terminals are connected in reverse of the required for series connection (n<N2). Let E0 be the emf of resulting battery and r0 be its internal resistance. Then
AE0=(N−n)E,r0=(N−n)rBE0=(N−2n)E,r0=(N−2n)rCE0=(N−2n)E,r0=NrDE0=(N−n)E,r0=NrN identical cells, each of emf ε and internal resistances r are joined in series. Out of these, n cells are wrongly connected, i.e. their terminals are connected in reverse order as required for series connection. If εo be the emf of the resulting battery and ro be its internal resistance then for n <N/2
Aε0=(N−n)ε,ro=(N−n)rBε0=(N−n)ε,ro=(N−2n)rCv εo=(N−2n)ε,ro=NrDεo=(N−n)ε,ro=NrIf n identical cells, each of emf E, are joined in series, the net emf is
AEnBnECn2EDnone of these
A group of six identical cells each of emf E and internal resistance r are joined in series to form a loop. The terminal voltage across each cells is
View SolutionA group of six identical cells each of emf E and internal resistance r are joined in series to form a loop. The terminal voltage across each cells is
View SolutionA group of six identical cells each of emf E and internal resistance r are joined in series to from a loop. The terminal voltage across each cell is
View SolutionA group of n identical cells each of EMF E and internal resistance r are joined in series to form a loop as shown . The terminal voltage across each cell is
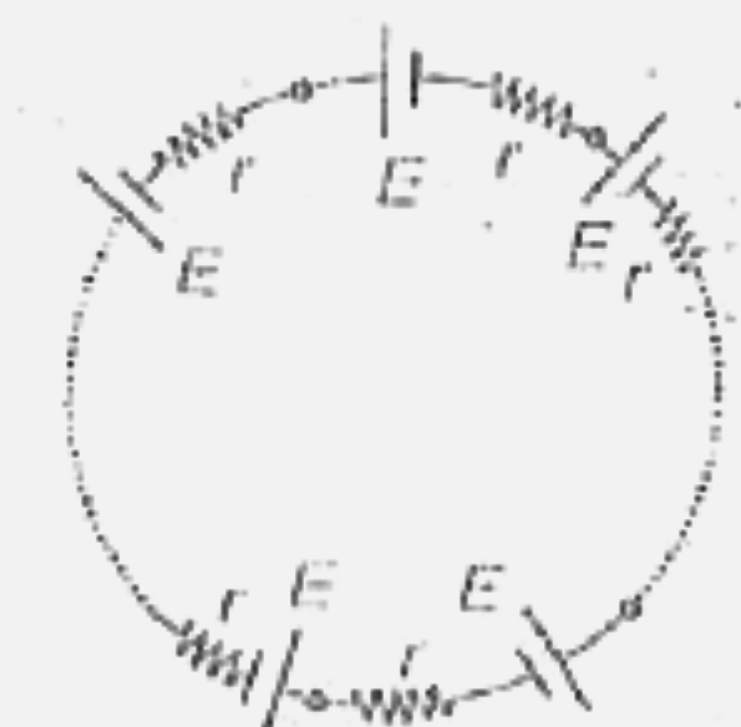
View SolutionSix cell each of emf E and internal resistance r are connected in series. If due to over sight, two cells are connected wrongly, then the equivalent emf and internal resistance of the combination is
View Solution
