N identical cells, each of emf ε and internal resistances r are joined in series. Out of these, n cells are wrongly connected, i.e. their terminals are connected in reverse order as required for series connection. If εo be the emf of the resulting battery and ro be its internal resistance then for n <N/2
ε0=(N−n)ε,ro=(N−n)r
ε0=(N−n)ε,ro=(N−2n)r
v εo=(N−2n)ε,ro=Nr
εo=(N−n)ε,ro=Nr
The correct Answer is:C
To solve the problem, we need to determine the effective electromotive force (emf) and internal resistance of a battery made up of N identical cells, where n cells are connected in reverse order.
1. Understanding the Configuration:
- We have N identical cells, each with an emf of ϵ and an internal resistance of r.
- Out of these N cells, n cells are connected in reverse order.
2. Calculating the Effective EMF:
- The total emf contributed by the correctly connected cells is (N−n)ϵ (since N - n cells are connected in the correct direction).
- The total emf contributed by the n incorrectly connected cells is −nϵ (since they are connected in reverse).
- Therefore, the effective emf ϵ0 of the resulting battery can be calculated as:
ϵ0=(N−n)ϵ−nϵ=(N−2n)ϵ
3. Calculating the Total Internal Resistance:
- The internal resistance of each cell is r.
- Since all cells are connected in series, the total internal resistance r0 of the battery is simply the sum of the internal resistances of all N cells:
r0=N⋅r
4. Final Expressions:
- Thus, we have:
ϵ0=(N−2n)ϵ
r0=N⋅r
Conclusion:
For n<N2, the effective emf and internal resistance of the battery are given by:
- Effective emf: ϵ0=(N−2n)ϵ
- Internal resistance: r0=N⋅r
- We have N identical cells, each with an emf of ϵ and an internal resistance of r.
- Out of these N cells, n cells are connected in reverse order.
- The total emf contributed by the correctly connected cells is (N−n)ϵ (since N - n cells are connected in the correct direction).
- The total emf contributed by the n incorrectly connected cells is −nϵ (since they are connected in reverse).
- Therefore, the effective emf ϵ0 of the resulting battery can be calculated as:
ϵ0=(N−n)ϵ−nϵ=(N−2n)ϵ
- The internal resistance of each cell is r.
- Since all cells are connected in series, the total internal resistance r0 of the battery is simply the sum of the internal resistances of all N cells:
r0=N⋅r
- Thus, we have:
ϵ0=(N−2n)ϵ
r0=N⋅r
For n<N2, the effective emf and internal resistance of the battery are given by:
- Effective emf: ϵ0=(N−2n)ϵ
- Internal resistance: r0=N⋅r
Similar Questions
n identical cells, each of emf E and internal resistance r, are joined in series to form a closed circuit. Find the potential difference across any one cell.
View SolutionA cell of emf ε and internal resistance r is charged by a current I, then
View Solutionn identical cells, each of emf E and internal resistance r, are joined in series to form a closed circuit. Find the potential difference across any one cell.
View SolutionIn a arrangement, 3n cells of emf ε and internal resistance r are connected in series. Out of 3n cells polarity of n cells is reversed. Current in the circuit is

View SolutionFour identical cells of emf ε and internal resistance r are to be connected in series. Suppose, if one of the cell is connected wrongly, then the equivalent emf and effective internal resistance of the combination is
View Solutionn identical cells, each of emf ε and internal resistance r, are joined in series to form a closed cirucit. One cell A is joined with reversed polarity. The potential difference across any one cell is
View SolutionA group of six identical cells each of emf E and internal resistance r are joined in series to form a loop. The terminal voltage across each cells is
View Solutionn identical cells each of e.m.f. E and internal resistance r are connected in series. An external resistance R is connected in series to this combination. The current through R is
View SolutionA group of n identical cells each of EMF E and internal resistance r are joined in series to form a loop as shown . The terminal voltage across each cell is
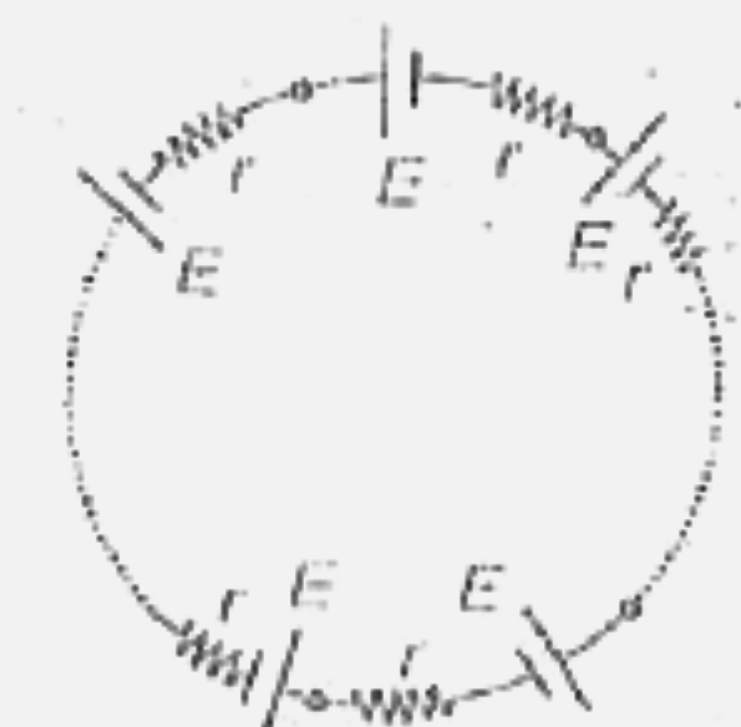
View SolutionFive cells each of emf E and internal resistance r are connecte in series. Due to oversight one cell is connected wrongly . The equivalent emf and internal resistance of the combination is
View Solution
