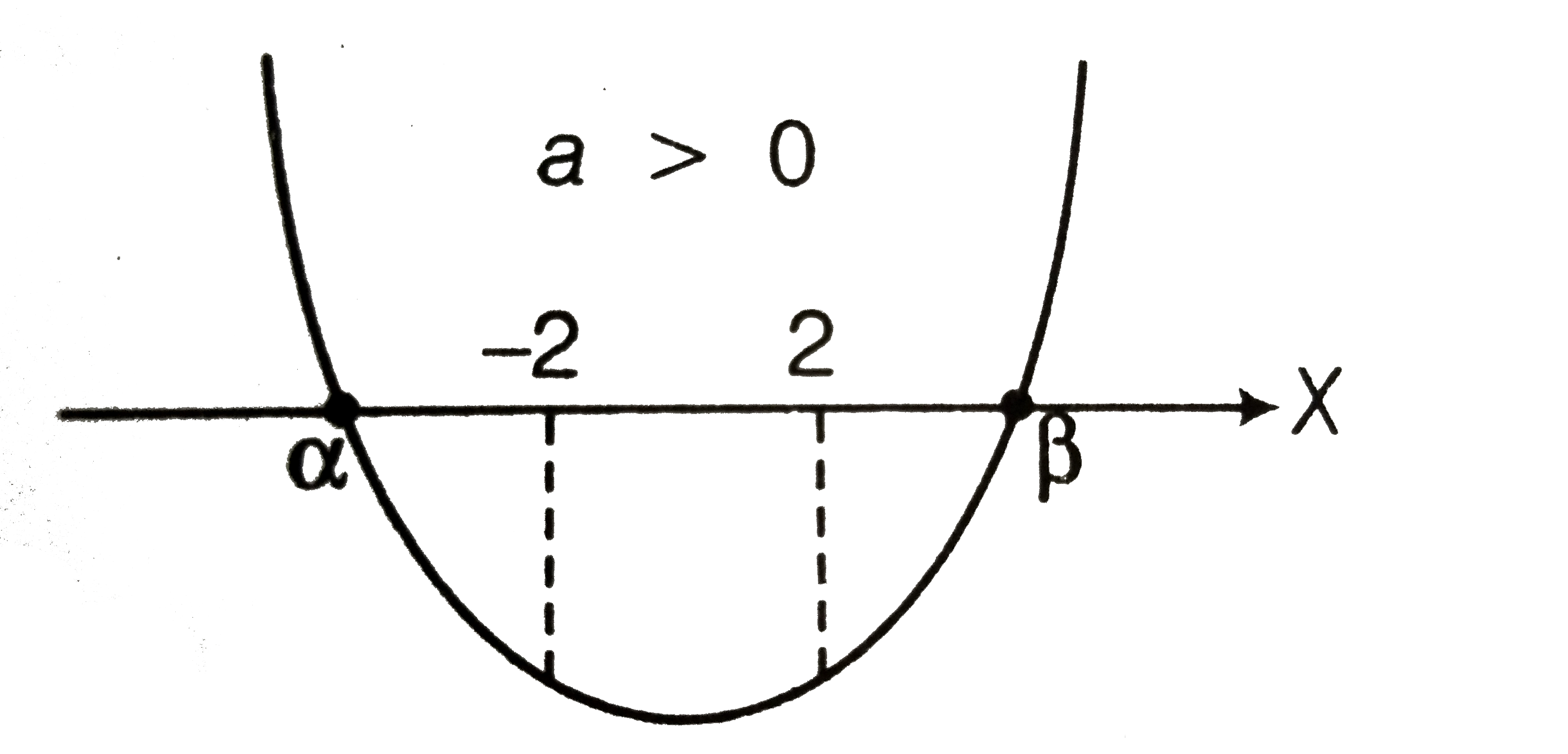
If the equation $a x^{2} + b x + c = 0 (a > 0)$ has two roots $α$ and $β$ such that $α < - 2$ and $β > 2$ , then Solution in Punjabi

A

$4 a - 2 | b | + c < 0$

B

$9 a - 3 | b | + c < 0$

C

$a - | b | + c < 0$

D

$c < 0, b^{2} - 4 a c > 0$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A, C, D

Here $D > 0$

$b^{2} - 4 a c > 0$
or $b^{2} > 4 a c$ …… i and $f (0) < 0$
$\Rightarrow c < 0$ ..ii
$f (1) < 0$
$\Rightarrow a + b + c < 0$ ………iii
$f (- 1) < 0$
$\Rightarrow a - b + c < 0$ ………..iv
$f (2) < 0$
$\Rightarrow 4 a + 2 b + c < 0$ ………v
$f (- 2) < 0$
$\Rightarrow 4 a - 2 b + c < 0$ ...............vi
From Eqs i and ii we get
$c < 0, b^{2} - 4 a c > 0$
From Eqs. (iii) and (iv) we get
$a - | b | + c < 0$
and from Eqs (v) and (vi) we get
$4 a - 2 | b | + c < 0$

Updated on:21/07/2023

|

Class 12 MATHS QUADRATIC EQUATIONS

Topper's Solved these Questions

Similar Questions

ARIHANT MATHS-THEORY OF EQUATIONS-Exercise (More Than One Correct Option Type Questions)

Home
Ask Doubt
Profile