Let x, y, z be elements from interval [0,2π] satisfying the inequality (4+sin4x)(2+cot2y)(1+sin4z)≤12sin2z , then Solution in Punjabi
the number of ordered pairs (x,y) is 5
the number of ordered pairs (y,z) is 8
the number of ordered pairs (z,x) is 8
the number of pairs (y,z) such that z=y is 2
The correct Answer is:C, D
Step by step video & image solution for Let x, y, z be elements from interval [0,2pi] satisfying the inequality (4+ sin 4 x )(2+ cot^(2) y)(1+ sin^(4) z) le 12 sin^(2) z , then by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- TRIGONOMETRIC EQUATIONS AND INEQUATIONSBOOK - ARIHANT MATHSCHAPTER - TRIGONOMETRIC EQUATIONS AND INEQUATIONSEXERCISE - Exercise (Passage Based Questions)
13 Videos
- TRIGONOMETRIC EQUATIONS AND INEQUATIONSBOOK - ARIHANT MATHSCHAPTER - TRIGONOMETRIC EQUATIONS AND INEQUATIONSEXERCISE - Trigonometric Equations and Inequations Exercise 3 :Passage Based Questions
1 Videos
- TRIGONOMETRIC EQUATIONS AND INEQUATIONSBOOK - ARIHANT MATHSCHAPTER - TRIGONOMETRIC EQUATIONS AND INEQUATIONSEXERCISE - Exercise (Single Option Correct Type Questions)
60 Videos
- THREE DIMENSIONAL COORDINATE SYSTEMBOOK - ARIHANT MATHSCHAPTER - THREE DIMENSIONAL COORDINATE SYSTEMEXERCISE - Three Dimensional Coordinate System Exercise 12 : Question Asked in Previous Years Exam
2 Videos
- TRIGONOMETRIC FUNCTIONS AND IDENTITIESBOOK - ARIHANT MATHSCHAPTER - TRIGONOMETRIC FUNCTIONS AND IDENTITIESEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
18 Videos
Similar Questions
If number of solution and sum of solution of the equation 3sin2x−7sinx+2=0,x∈[0,2π] are respectively N and S and fn(θ)=sinnθ+cosnθ. On the basis of above information , answer the following questions.
Value of N is
View SolutionIf an angle and a side of a right angle triangle is known , then rest of the sides and angles can be found as follows
In ΔABC(figure ), if ∠B=90∘,∠C=θandBC=x, then AB=xtanθandAC=xsecθ .
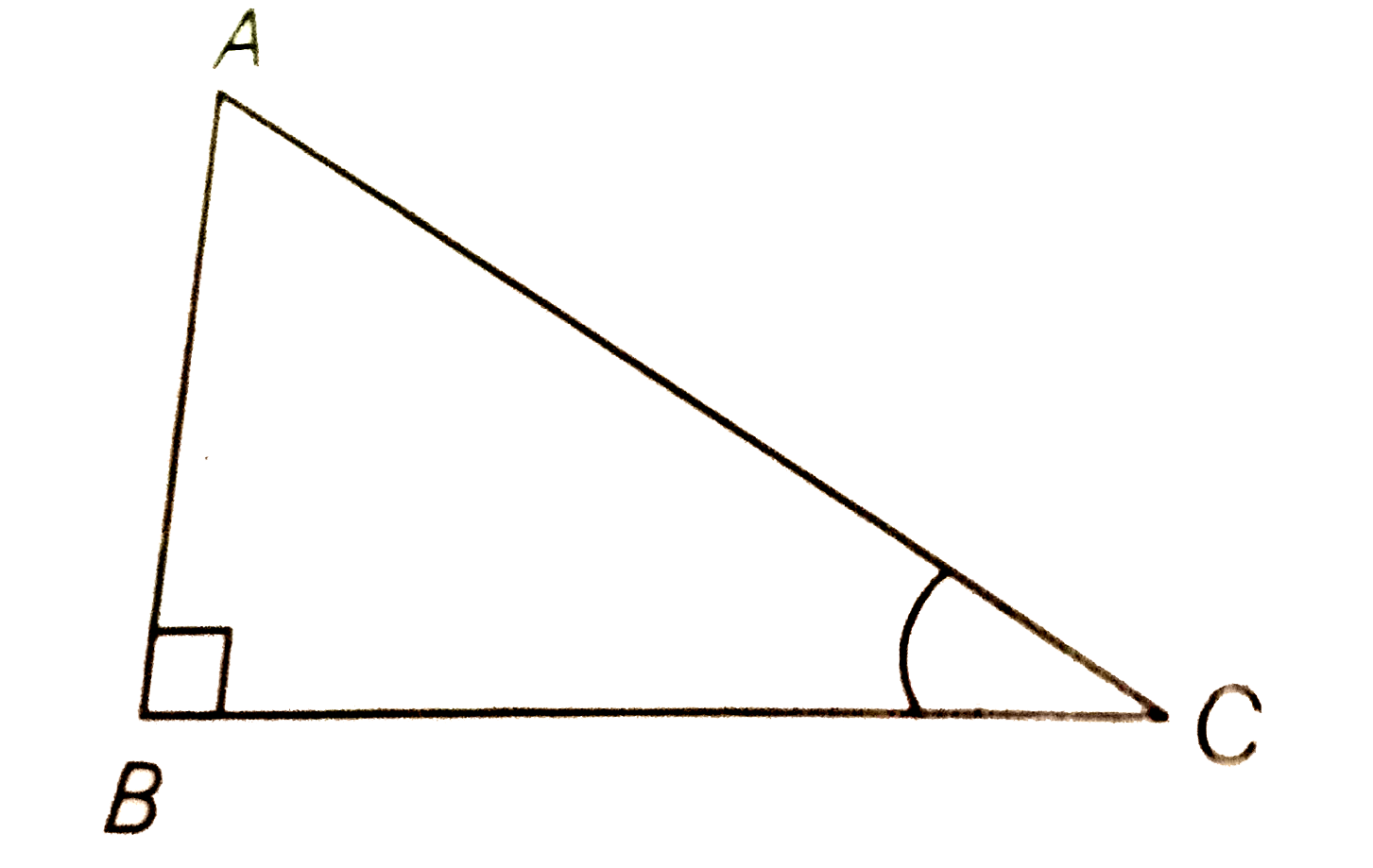
Now, consider in isosceles triangle PQR (Figure 2),
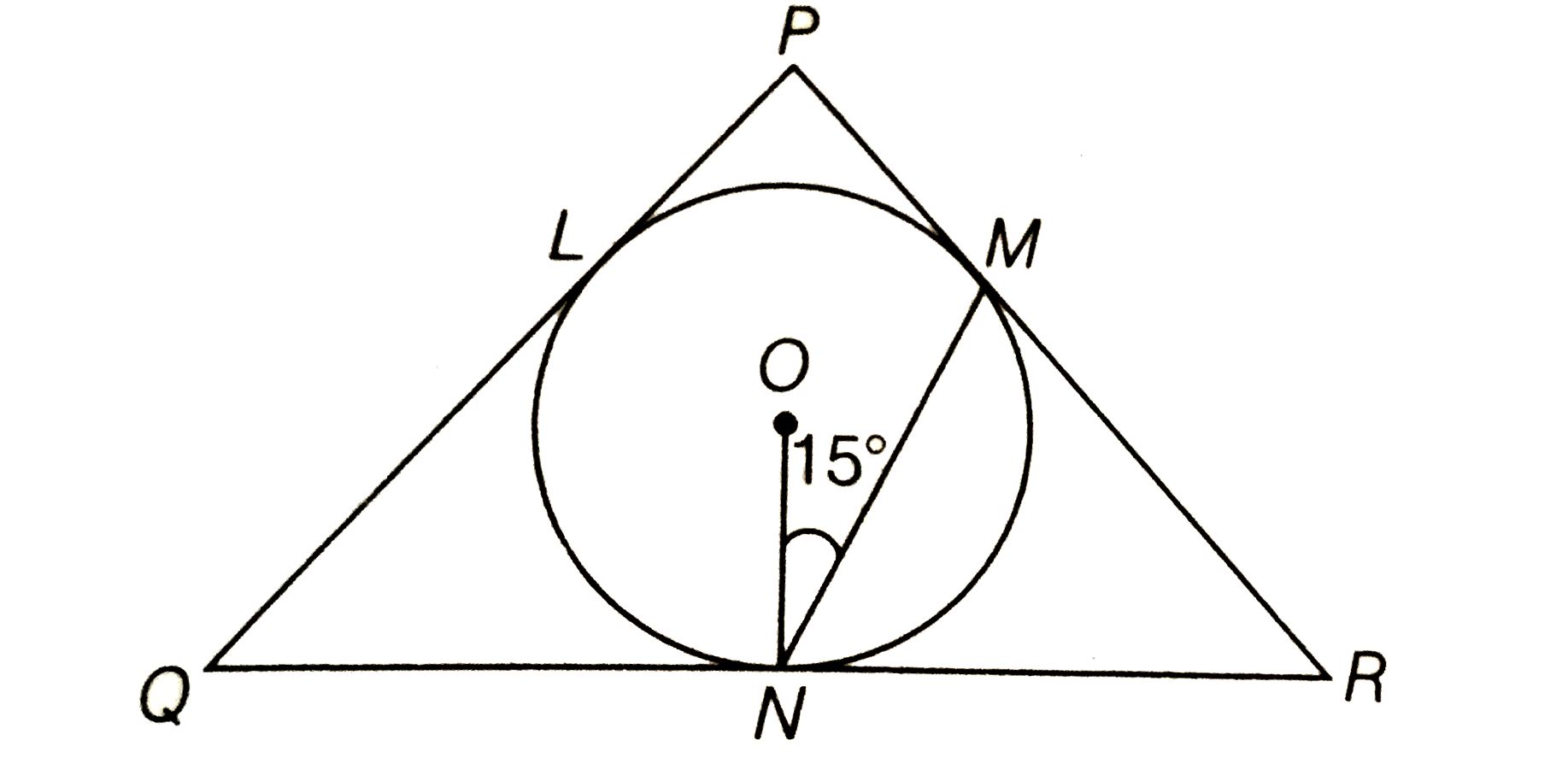
Where PQ=PR and 20N=√3
On the basis of the above information answer the question
The angle of triangle PQR are
View SolutionShow that sinx−sinycosx+cosy=tan(x−y2)
View SolutionConsider the line L1:x−12=y−1=z+31,L2:x−41=y+31=z+32 find the angle between them.
View SolutionLet αandβ be non-zero real numbers such that 2(cosβ−cosα)+cosαcosβ=1. Then which of the following is/are true ?
View SolutionIf sin ^ (- 1) x + sin ^ (- 1) y + sin ^ (- 1) z = pi show that, x ^ (4) + y ^ (4) + z ^ (4) + 4x ^ ( 2) y ^ (2) z ^ (2) = 2 (x ^ (2) y ^ (2) + y ^ (2) z ^ (2) + z ^ (2) x ^ (2))
View SolutionIf sin ^ (- 1) x + sin ^ (- 1) y + sin ^ (- 1) z = pi, show that x ^ (4) + y ^ (4) + z ^ (4) + 4x ^ ( 2) y ^ (2) z ^ (2) = 2 (x ^ (2) y ^ (2) + y ^ (2) z ^ (2) + z ^ (2) x ^ (2))
View SolutionIf sin ^ (- 1) x + sin ^ (- 1) y + sin ^ (- 1) z = pi then x ^ (4) + y ^ (4) + z ^ (4) + 4x ^ (2) y ^ (2) z ^ (2)
View SolutionIf sin ^ (- 1) x + sin ^ (- 1) y + sin ^ (- 1) z = pi then x ^ (4) + y ^ (4) + z ^ (4) + 4x ^ (2) y ^ (2) z ^ (2) =
View SolutionLet N be the number of triplets (x,y,z) where x,y,z in[0,2 pi] satisfying the inequality (4+sin4x)(2+cot^(2)-y)(1+sin^(4)+z)<12sin^(2)-z Find the value of (N)/(2)
View Solutionयदि sin−1x+sin−1y+sin−1z=π सिद्ध कीजिए कि x4+y4+z4+4x2y2z2=2(x2y2+y2z2+z2x2)
View Solutionif sin−1x+sin−1y+sin−1z=π show that ,
x4+y4+z4+4x2y2z2=2(x2y2+y2z2+z2x2)
View SolutionIf Sin−1x+Sin−1y+Sin−1z=π, then prove that x4+y4+z4+4x2y2z2=2(x2y2+y2z2+z2x2).
View SolutionIf sin−1x+sin−1y+sin−1z=3π2, then A=x2+y2+z2.
(sin−1x)2+(sin−1y)2+(sin−1z)2=3π24, then B=∣∣(x+y+z)min∣∣. Then the value of (A+B) is _____________ .
View SolutionIF sin−1X+sin−1y+sin−1z=π, then prove that x4+y4+z4+4x2y2z2=2(x2y2+y2z2+z2x2).
View SolutionIf sin−1x+sin−1y+sin−1z=π, then prove that x4+y4+z4+4x2y2z2=2(x2y2+y2z2+z2x2)
View Solution
