Let f be a differentiable function on the open interval(a, b). Which of the following statements must be true?
(i) f is continuous on the closed interval [a,b],
(ii) f is bounded on the open interval (a,b)
(iii)If a < a1< b1 < b, and f(a1) < 0 < f(b1), then there is a number c such that a1 < c < b, and f(c) = 0
(a)Only I and II
(b)Only I and III
(c)Only II and III
(d)Only III
Solution in Punjabi
Only I and II
Only I and III
Only II and III
Only III
The correct Answer is:D
Step by step video & image solution for Let f be a differentiable function on the open interval(a, b). Which of the following statements must be true? (i) f is continuous on the closed interval [a,b], (ii) f is bounded on the open interval (a,b) (iii)If a < a1< b1 < b, and f(a1) < 0 < f(b1), then there is a number c such that a1 < c < b, and f(c) = 0 (a)Only I and II (b)Only I and III (c)Only II and III (d)Only III by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CONTINUITY AND DIFFERENTIABILITYBOOK - ARIHANT MATHSCHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - Exercise (More Than One Correct Option Type Questions)
26 Videos
- CONTINUITY AND DIFFERENTIABILITYBOOK - ARIHANT MATHSCHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - Exercise (Statement I And Ii Type Questions)
11 Videos
- CONTINUITY AND DIFFERENTIABILITYBOOK - ARIHANT MATHSCHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - Exercise For Session 7
10 Videos
- COMPLEX NUMBERSBOOK - ARIHANT MATHSCHAPTER - COMPLEX NUMBERSEXERCISE - Complex Number Exercise 8
3 Videos
- COORDINATE SYSTEM AND COORDINATES BOOK - ARIHANT MATHSCHAPTER - COORDINATE SYSTEM AND COORDINATES EXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
7 Videos
Similar Questions
Function whose jump (non-negative difference of LHL and RHL) of discontinuity is greater than or equal to one. Is/are
View SolutionStatement I f(x)=sinx+[x] is discontinuous at x = 0.
Statement II If g(x) is continuous and f(x) is discontinuous, then g(x) + f(x) will necessarily be discontinuous at x = a.
View SolutionNumber of points of non-differerentiable of f(x)=sinπ(x−[x])in (−π/2,[π/2). Where [.] denotes the greatest integer function is
View SolutionFind the modules of 2+3ι
View SolutionIf a vertex of a triangle is (1, 1) and the mid-points of two side through this vertex are (-1, 2) and (3, 2), then centroid of the triangle is
View SolutionLet f be a differentiable function on the open interval(a,b).Which of the following statements must be true? (i) f is continuous on the closed interval [a,b],( ii) f is bounded on the open interval (a,b)
View SolutionStatement 1: If both functions f(t)andg(t) are continuous on the closed interval [1,b], differentiable on the open interval (a,b) and g′(t) is not zero on that open interval, then there exists some c in (a,b) such that f′(c)g′(c)=f(b)−f(a)g(b)−g(a) Statement 2: If f(t)andg(t) are continuou and differentiable in [a, b], then there exists some c in (a,b) such that f′(c)=f(b)−f(a)b−aandg′(c)g(b)−g(a)b−a from Lagranes mean value theorem.
View SolutionIn a ΔABC, If ∣∣ ∣∣1ab1ca1bc∣∣ ∣∣=0, then sin2A+sin2B+sin2C is
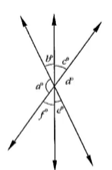
View SolutionIn Figure, which of the following statements must be true? (i) a+b=d+c (ii) a+c+e=1800 (iii) b+f=c+e (a) (i) only (b) (ii) only (c) (iii) only (d) (ii) and (iii) only
View SolutionLet f(x), be a function which is continuous in closed interval [0,1] and differentiable in open interval 10,1[ Show that EE a point c in]0,1[ such that f'(c)=f(1)-f(0)
View Solutionयदि फलन f'(x) और g(x) बंद अंतराल [ab] में संतत हो तथा खुले अंतराल (a,b) में अवकलनीय हो तो दिखाए की काम-से-कम एक ऐसा c मिलेगा जहां a<c<b ताकि
∣∣∣f(a)f(b)g(a)g(b)∣∣∣=(b−a)∣∣∣f(a)f'(c)g(a)g'(c)∣∣∣
View SolutionIf f is an odd function and f(a)=b, which of the following must also be true ?
I. f(a)=−b
II.f(−a)=b
III. f(−a)=−b
View SolutionWhich of the following is arranged in increasing order of ionic mobility of ions in their aqueous solutions?
(A) \(I^{-} < Br^{-} < Cl^{-} < F^{-}\)
(B) \(F^{-} < Cl^{-} < Br^{-} < I^{-}\)
(C) \(F^{-} < I^{-} < Cl^{-} < Br^{-}\)
(D) \(F^{-} < Cl^{-} < I^{-} < Br^{-}\)
View SolutionThe order of reactivity of halogens is
(A) F>Cl>Br>I
(B) F < Cl < Br < I
(C) F < Cl > Br < I
(D) F < Cl < Br> I
View SolutionPARAGRAPH : If function f,g are continuous in a closed interval [a,b] and differentiable in the open interval (a,b) then there exists a number c in (a,b) such that [g(b)-g(a)]f'(c)=[f(b)-f(a)]g'(c) If f(x)=ex and g(x)=e−x,a≤x≤b c=
View SolutionStatement 1: If both functions f(t)andg(t) are continuous on the closed interval [a,b], differentiable on the open interval (a,b) and g′(t) is not zero on that open interval, then there exists some c in (a,b) such that f′(c)g′(c)=f(b)−f(a)g(b)−g(a) Statement 2: If f(t)andg(t) are continuous and differentiable in [a, b], then there exists some c in (a,b) such that f′(c)=f(b)−f(a)b−aandg′(c)g(b)−g(a)b−a from Lagranges mean value theorem.
View Solution
