Statement I f(x)=sinx+[x] is discontinuous at x = 0.
Statement II If g(x) is continuous and f(x) is discontinuous, then g(x) + f(x) will necessarily be discontinuous at x = a. Solution in Punjabi
Statement I is correct, Statement II is also correct, Statement II is the correct explanation of Statement I
Statement I is correct, Statement II is also correct, Statement II is not the correct explanation of Statement I
Statement I is correct, Statement II is incorrect
Statement I is incorrect, Statement II is correct.
The correct Answer is:A
Step by step video & image solution for Statement I f(x) = sin x + [x] is discontinuous at x = 0. Statement II If g(x) is continuous and f(x) is discontinuous, then g(x) + f(x) will necessarily be discontinuous at x = a. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CONTINUITY AND DIFFERENTIABILITYBOOK - ARIHANT MATHSCHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - EXERCISE 4
3 Videos
- CONTINUITY AND DIFFERENTIABILITYBOOK - ARIHANT MATHSCHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - Exercise (Passage Based Questions)
16 Videos
- CONTINUITY AND DIFFERENTIABILITYBOOK - ARIHANT MATHSCHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - Exercise (More Than One Correct Option Type Questions)
26 Videos
- COMPLEX NUMBERSBOOK - ARIHANT MATHSCHAPTER - COMPLEX NUMBERSEXERCISE - Complex Number Exercise 8
3 Videos
- COORDINATE SYSTEM AND COORDINATES BOOK - ARIHANT MATHSCHAPTER - COORDINATE SYSTEM AND COORDINATES EXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
7 Videos
Similar Questions
A man leaves his home early in the morning to have a walk. He arrives at a junction of roads A and B as shown in figure. He takes the following steps in later journies :
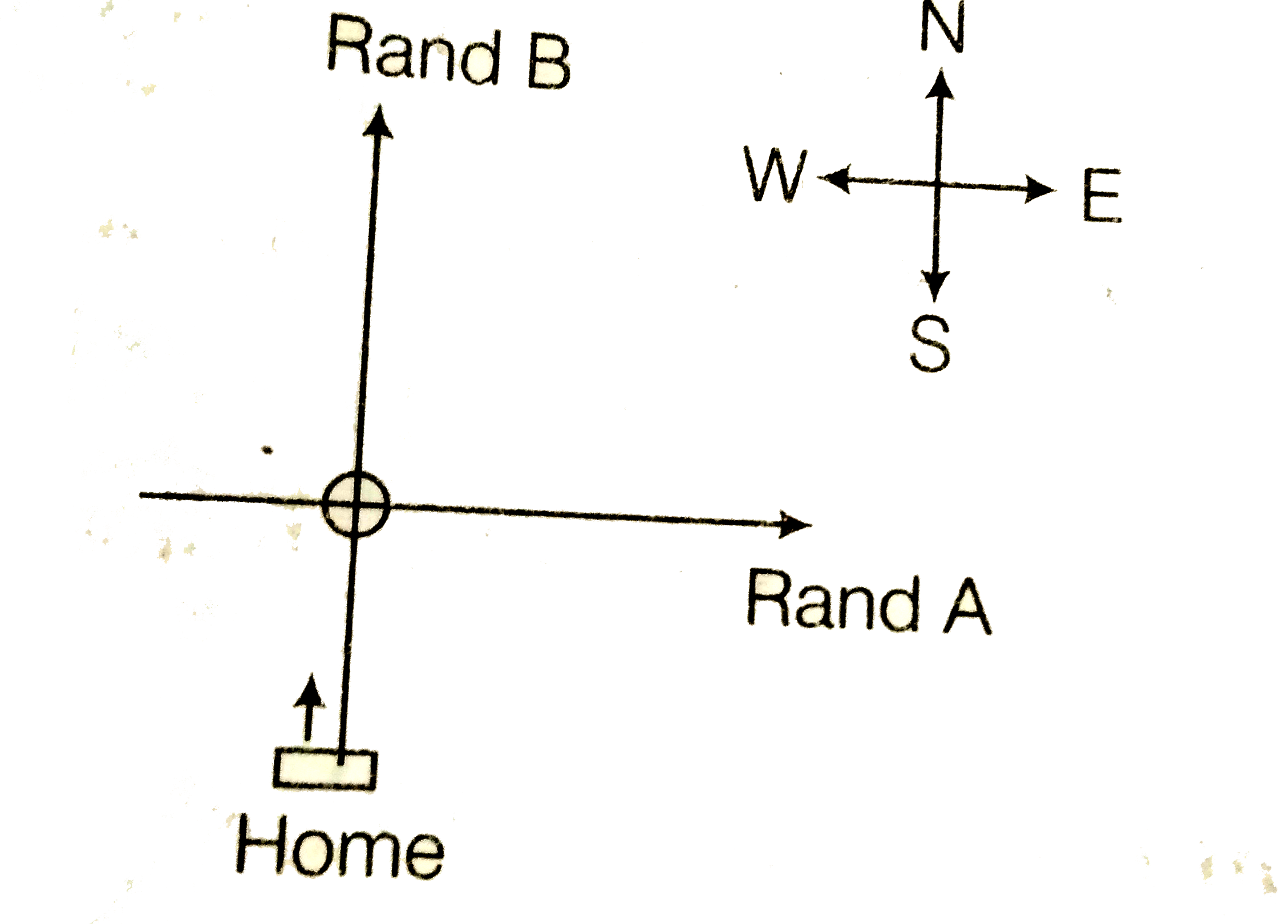
(i) 1 km in North direction.
(ii) Changes direction and moves in North-East direction for 2√2 km.
(iii) Changes direction and moves Southwards for distance of 2 km.
(iv) Finally he changes the direction and moves in South-East direction to reach road A again.
Now if roads A and B are taken as X-axis and y-axis ,then visible point representing the graph of y=f(x)
Then the value of x at which function f(x) is discontinous
View SolutionLet f be a function that is differentiable everywhere and that has the follwong properties :
(i) f(x)>0
(ii) f'(0)=−1
(iii) f(−x)=1f(x)andf(x+h)=f(x).f(h)
A standard result is f'(x)f(x)dx=log|f(x)|+C
The range fo the function Δ=f(|x|) is
View SolutionFunction whose jump (non-negative difference of LHL and RHL) of discontinuity is greater than or equal to one. Is/are
View SolutionFind the modules of 2+3ι
View SolutionIf a vertex of a triangle is (1, 1) and the mid-points of two side through this vertex are (-1, 2) and (3, 2), then centroid of the triangle is
View SolutionLet f(x)=[x], where [.] is the greatest integer fraction and g(x)=sin x be two valued functions over R. Which of the following statements is correct? (a) Both f(x) and g(x) are continuous at x=0 (b) f(x) is continuous at x=0, but g(x) is not continuous at x=0. (c) g(x) is continuous at x=0, but f(x) is not continuous at x=0. (d) Both f(x) and g(x) are discontinuous at x=0
View SolutionStatement 1: f(x)=cosx is continous at x=0andg(x)=[tanx],w h e r e[.] represents greatest integer function, is discontinuous at x=0,thenh(x)=f(x).g(x) is discontinuous at x=0. Statement 2: If f(x) is continous and g(x) is discontinuous at x=a,thenh(x)=f(x)g(x) is discontinuous at x=a
View SolutionWhich of the following statements is always true? ([.] represents the greatest integer function. a) If f(x) is discontinuous then |f(x)| is discontinuous b) If f(x) is discontinuous then f(|x|) is discontinuous c) f(x)=[g(x)] is discontinous when g(x) is an integer d) none of these
View SolutionIf f(x)={sin((1)/(x)),x!=00,x=0 then it is discontinuous at-
View SolutionIf f(x)=(1)/((1-x)) and g(x)=f[f{f(x))} then g(x) is discontinuous at
View SolutionIf f(x) be continuous function and g(x) be discontinuous, then
View Solutionयदि f(x) एक संतत फलन है और g(x) एक असंतत फलन है तो सिद्ध करें कि f(x)+g(x) एक असंतत फलन है।
View SolutionIf α,β (where α<β) are the points of discontinuity of the function g(x) = f(f(f(x))), where f(x) = (1)/(1-x). Then, The points of discontinuity of g(x) is
View SolutionStatement I f(x)=sinx+[x] is discontinuous at x = 0.
Statement II If g(x) is continuous and f(x) is discontinuous, then g(x) + f(x) will necessarily be discontinuous at x = a.
View SolutionIf the function f:R→Randg:R→R are such that f(x) is continuous at x=α and f(α)=aandg(x) is discontinuous at x = a but g(f(x)) is continuous at x=α, then (f(x) and g(x) are non - constant functions)
View SolutionIf f(x) = sgn (x) and g (x) = (1−x2),then the number of points of discontinuity of function f (g (x)) is -
View Solution
