Let f be a function that is differentiable everywhere and that has the follwong properties :
(i) f(x)>0
(ii) f'(0)=−1
(iii) f(−x)=1f(x)andf(x+h)=f(x).f(h)
A standard result is f'(x)f(x)dx=log|f(x)|+C
Range of f(x) is Solution in Punjabi
The correct Answer is:A
Step by step video & image solution for Let f be a function that is differentiable everywhere and that has the follwong properties : (i) f(x) gt 0 (ii) f'(0) = -1 (iii) f(-x) = (1)/(f(x))and f(x+h)=f(x).f(h) A standard result is (f'(x))/(f(x))dx = log|f(x)| + C Range of f(x) is by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CONTINUITY AND DIFFERENTIABILITYBOOK - ARIHANT MATHSCHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - EXERCISE 5
3 Videos
- CONTINUITY AND DIFFERENTIABILITYBOOK - ARIHANT MATHSCHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - Exercise (Single Integer Answer Type Questions)
9 Videos
- CONTINUITY AND DIFFERENTIABILITYBOOK - ARIHANT MATHSCHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - EXERCISE 4
3 Videos
- COMPLEX NUMBERSBOOK - ARIHANT MATHSCHAPTER - COMPLEX NUMBERSEXERCISE - Complex Number Exercise 8
3 Videos
- COORDINATE SYSTEM AND COORDINATES BOOK - ARIHANT MATHSCHAPTER - COORDINATE SYSTEM AND COORDINATES EXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
7 Videos
Similar Questions
Find dydxify=2x−3
View SolutionNumber of points of discontinuity of f(x)=tan2x−sec2x in (0,2π) is
View SolutionA man leaves his home early in the morning to have a walk. He arrives at a junction of roads A and B as shown in figure. He takes the following steps in later journies :
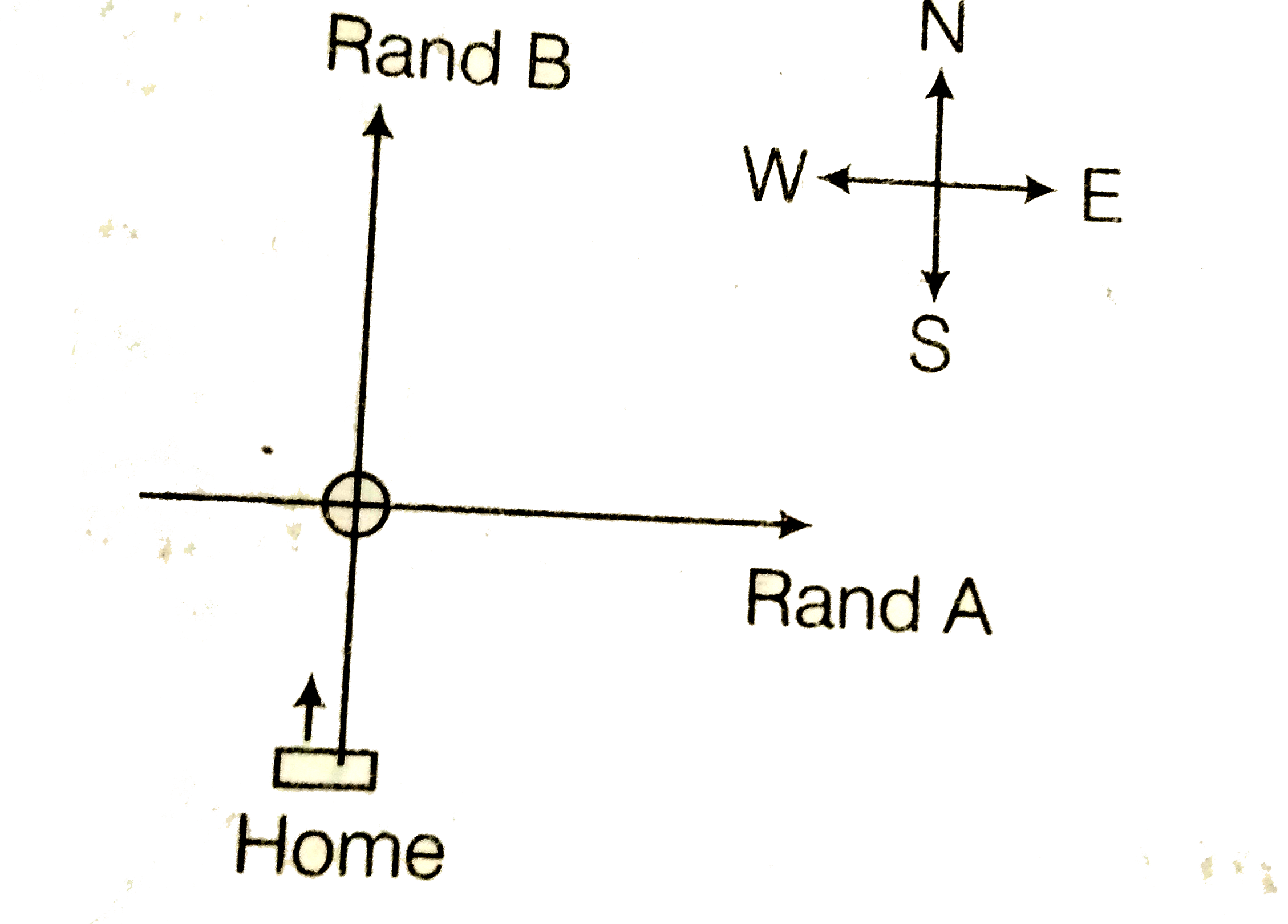
(i) 1 km in North direction.
(ii) Changes direction and moves in North-East direction for 2√2 km.
(iii) Changes direction and moves Southwards for distance of 2 km.
(iv) Finally he changes the direction and moves in South-East direction to reach road A again.
Now if roads A and B are taken as X-axis and y-axis ,then visible point representing the graph of y=f(x)
Then the value of x at which function f(x) is discontinous
View SolutionFind the modules of 2+3ι
View SolutionIf a vertex of a triangle is (1, 1) and the mid-points of two side through this vertex are (-1, 2) and (3, 2), then centroid of the triangle is
View SolutionLet f be a twice differentiable function such that
f''(x)=−f(x) and f'(x)=g(x).If h'(x)=[f(x)]2+[g(x)]2,
h(a)=8 and h(0)=2, then h(2)=
View SolutionLet f be a function that is differentiable everywhere and that has the follwong properties :
(i) f(x)>0
(ii) f'(0)=−1
(iii) f(−x)=1f(x)andf(x+h)=f(x).f(h)
A standard result is f'(x)f(x)dx=log|f(x)|+C
Range of f(x) is
View SolutionLet f be a function that is differentiable everywhere and that has the follwong properties :
(i) f(x)>0
(ii) f'(0)=−1
(iii) f(−x)=1f(x)andf(x+h)=f(x).f(h)
A standard result is f'(x)f(x)dx=log|f(x)|+C
The function y = f(x) is
View SolutionLet f be a function that is differentiable everywhere and that has the follwong properties :
(i) f(x)>0
(ii) f'(0)=−1
(iii) f(−x)=1f(x)andf(x+h)=f(x).f(h)
A standard result is f'(x)f(x)dx=log|f(x)|+C
If h(x) = f'(x), then h(x) is given by
View SolutionLet f be a differentiable function satisfying f(xy)=f(x).f(y).∀x>0,y>0 and f(1+x)=1+x{1+g(x)}, where limx→0g(x)=0 then ∫f(x)f'(x)dx is equal to
View SolutionLet f be a function such that f(x+f(y))=f(f(x))+f(y) ∀x,y∈R and f(h)=h for 0ε
where ε>0, then determine f'(x) and f(x).
View SolutionLet f(x) ={x+1:x£0x:x>0 and h (x) = |f(x) + f(|x|) . Then h(x) is defined by :
View SolutionIF f(x), f'(x) f''(x) are positive functions and f(0)=1, f')0)=2 then the solution of the differential equation ∣∣∣f(x)f'(x)f'(x)f''(x)∣∣∣=0 is
View SolutionLet f(x)>0 for all x and f'(x) exists for all x. If f is the inverse functin of h and h'(x)=11+logx. Then f'(x) will be
View Solutionf(x) is a continuous and differentiable function.
f'(x)≠0and∣∣∣f'(x)f(x)f''(x)f'(x)∣∣∣=0. If f(0)=1 and f'(0)=2 then f(x)=....
View SolutionStatement True/ False: br If f(x)>0 then the function f(x) is said to be decreasing.
View Solution
