Let y = f(x) be defined in [a, b], then
(i) Test of continuity at x=c,a<c<b
(ii) Test of continuity at x = a
(iii) Test of continuity at x = b
Case I Test of continuity at x=c,a<c<b
If y = f(x) be defined at x = c and its value f(c) be equal to limit of f(x) as x→c i.e. f(c) = limx→cf(x)
or limx→c−f(x)=f(c)=limx→c+f(x)
or LHL = f(c) = RHL
then, y = f(x) is continuous at x = c.
Case II Test of continuity at x = a
If RHL = f(a)
Then, f(x) is said to be continuous at the end point x = a
Case III Test of continuity at x = b, if LHL = f(b)
Then, f(x) is continuous at right end x = b.
Max ([x],|x|) is discontinuous at Solution in Punjabi
x = 0
ϕ
x=n,n∈I
None of these
The correct Answer is:B
Step by step video & image solution for Let y = f(x) be defined in [a, b], then (i) Test of continuity at x = c, a lt c lt b (ii) Test of continuity at x = a (iii) Test of continuity at x = b Case I Test of continuity at x = c, a lt c lt b If y = f(x) be defined at x = c and its value f(c) be equal to limit of f(x) as x rarr c i.e. f(c) = lim_(x to c) f(x) or lim_(x to c^(-))f(x) = f(c) = lim_(x to c^(+)) f(x) or LHL = f(c) = RHL then, y = f(x) is continuous at x = c. Case II Test of continuity at x = a If RHL = f(a) Then, f(x) is said to be continuous at the end point x = a Case III Test of continuity at x = b, if LHL = f(b) Then, f(x) is continuous at right end x = b. Max ([x],|x|) is discontinuous at by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - ARIHANT MATHSCHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - EXERCISE 53videos
CONTINUITY AND DIFFERENTIABILITY
- BOOK - ARIHANT MATHSCHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - Exercise (Single Integer Answer Type Questions)9videos
CONTINUITY AND DIFFERENTIABILITY
- BOOK - ARIHANT MATHSCHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - EXERCISE 43videos
CONTINUITY AND DIFFERENTIABILITY
- BOOK - ARIHANT MATHSCHAPTER - COMPLEX NUMBERSEXERCISE - Complex Number Exercise 83videos
COMPLEX NUMBERS
- BOOK - ARIHANT MATHSCHAPTER - COORDINATE SYSTEM AND COORDINATES EXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)7videos
COORDINATE SYSTEM AND COORDINATES
Similar Questions
Find dydxify=2x−3
04:04View SolutionNumber of points of discontinuity of f(x)=tan2x−sec2x in (0,2π) is
02:18View SolutionA man leaves his home early in the morning to have a walk. He arrives at a junction of roads A and B as shown in figure. He takes the following steps in later journies :
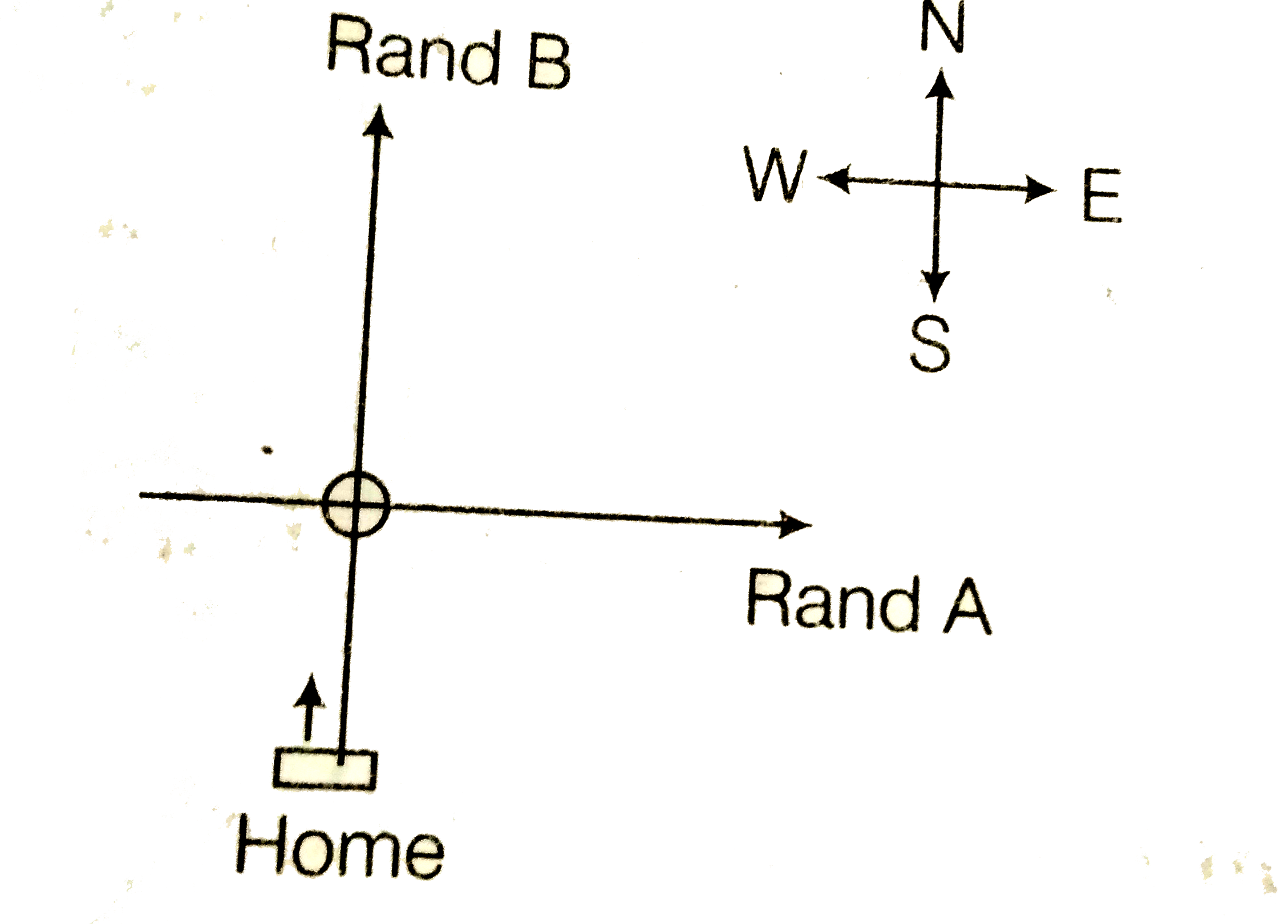
(i) 1 km in North direction.
(ii) Changes direction and moves in North-East direction for 2√2 km.
(iii) Changes direction and moves Southwards for distance of 2 km.
(iv) Finally he changes the direction and moves in South-East direction to reach road A again.
Now if roads A and B are taken as X-axis and y-axis ,then visible point representing the graph of y=f(x)
Then the value of x at which function f(x) is discontinous03:14View SolutionFind the modules of 2+3ι
02:38View SolutionIf a vertex of a triangle is (1, 1) and the mid-points of two side through this vertex are (-1, 2) and (3, 2), then centroid of the triangle is
02:50View SolutionLet f(x)=|x| . Then, for all x f is continuous (b) f is differentiable for some x (c) f ' is continuous (d) f is continuous
02:26View SolutionIf f(x) is twice differentiable and continuous function in x∈[a,b] also f'(x)>0 and f''(x)<0 and c in (a,b) then f(c)−f(a)f(b)−f(a) is greater than
03:04View SolutionLet y = f(x) be defined in [a, b], then
(i) Test of continuity at x=c,a<c<b
(ii) Test of continuity at x = a
(iii) Test of continuity at x = b
Case I Test of continuity at x=c,a<c<b
If y = f(x) be defined at x = c and its value f(c) be equal to limit of f(x) as x→c i.e. f(c) = limx→cf(x)
or limx→c−f(x)=f(c)=limx→c+f(x)
or LHL = f(c) = RHL
then, y = f(x) is continuous at x = c.
Case II Test of continuity at x = a
If RHL = f(a)
Then, f(x) is said to be continuous at the end point x = a
Case III Test of continuity at x = b, if LHL = f(b)
Then, f(x) is continuous at right end x = b.
If f(x)=⎧⎪ ⎪ ⎪ ⎪⎨⎪ ⎪ ⎪ ⎪⎩sinx,x≤0tanx,0<x<2πcosx,2π≤x<3π3π,x=3π, then f(x) is discontinuous at06:47View SolutionLet y = f(x) be defined in [a, b], then
(i) Test of continuity at x=c,a<c<b
(ii) Test of continuity at x = a
(iii) Test of continuity at x = b
Case I Test of continuity at x=c,a<c<b
If y = f(x) be defined at x = c and its value f(c) be equal to limit of f(x) as x→c i.e. f(c) = limx→cf(x)
or limx→c−f(x)=f(c)=limx→c+f(x)
or LHL = f(c) = RHL
then, y = f(x) is continuous at x = c.
Case II Test of continuity at x = a
If RHL = f(a)
Then, f(x) is said to be continuous at the end point x = a
Case III Test of continuity at x = b, if LHL = f(b)
Then, f(x) is continuous at right end x = b.
Number of points of discontinuity of [2x3−5] in [1, 2) is (where [.] denotes the greatest integral function.)05:12View SolutionLet y = f(x) be defined in [a, b], then
(i) Test of continuity at x=c,a<c<b
(ii) Test of continuity at x = a
(iii) Test of continuity at x = b
Case I Test of continuity at x=c,a<c<b
If y = f(x) be defined at x = c and its value f(c) be equal to limit of f(x) as x→c i.e. f(c) = limx→cf(x)
or limx→c−f(x)=f(c)=limx→c+f(x)
or LHL = f(c) = RHL
then, y = f(x) is continuous at x = c.
Case II Test of continuity at x = a
If RHL = f(a)
Then, f(x) is said to be continuous at the end point x = a
Case III Test of continuity at x = b, if LHL = f(b)
Then, f(x) is continuous at right end x = b.
Max ([x],|x|) is discontinuous at07:28View SolutionIf a<b then f(x) =sqrt ((x-a)/(b-x)) is continuous on
05:30View SolutionWhich of the following order is correct among the following ?
C−X Bond length order is
H3C−F<CH3C−Cl<H3C−Br<H3C−l
( ii) C- X Bond enthalapies order is
H3C−Cl>H3C−F>CH3−Br>CH3−I
(III) C-X Bond dipole moment order is
H3C−Cl>H3C−F>CH3−Br>CH3−I04:54View Solutioncontinuous at x = 0
Let f(x)=⎧⎪ ⎪ ⎪⎨⎪ ⎪ ⎪⎩(1+|sinx|)a|sinx|−π6<x<0bx=0etan2x/tan3x0<x<π6
Determine a and b such that f(x) continuous at x = 0 .02:42View Solutionf(x) is continuous on [a.b] then
Statemant- I : Ltx→a+f(x)=f(a)
Statement-II : f is continuous for every x in (a,b)
Statement-III Ltx→b−f(x)=f(b)
Which of the following is true02:10View SolutionLet y = f(x) be defined in [a, b], then
(i) Test of continuity at x=c,a<c<b
(ii) Test of continuity at x = a
(iii) Test of continuity at x = b
Case I Test of continuity at x=c,a<c<b
If y = f(x) be defined at x = c and its value f(c) be equal to limit of f(x) as x→c i.e. f(c) = limx→cf(x)
or limx→c−f(x)=f(c)=limx→c+f(x)
or LHL = f(c) = RHL
then, y = f(x) is continuous at x = c.
Case II Test of continuity at x = a
If RHL = f(a)
Then, f(x) is said to be continuous at the end point x = a
Case III Test of continuity at x = b, if LHL = f(b)
Then, f(x) is continuous at right end x = b.
If f(x)=⎧⎪ ⎪ ⎪ ⎪⎨⎪ ⎪ ⎪ ⎪⎩sinx,x≤0tanx,0<x<2πcosx,2π≤x<3π3π,x=3π, then f(x) is discontinuous at03:02View Solution

