Let f(x)=max{1+sinx,1,1−cosx},x∈[0,2π],andg(x)=max{1,|x−1|},x∈R. ThenSolution in Punjabi
Step by step video & image solution for Let f(x)=max{1+sinx,1,1-cosx}, x in [0,2pi], and g(x)=max{1,|x-1|}, x in R. Then by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - ARIHANT MATHSCHAPTER - FUNCTIONSEXERCISE - Exercise For Session 15videos
FUNCTIONS
- BOOK - ARIHANT MATHSCHAPTER - FUNCTIONSEXERCISE - Exercise For Session 26videos
FUNCTIONS
- BOOK - ARIHANT MATHSCHAPTER - ESSENTIAL MATHEMATICAL TOOLS EXERCISE - Exercise (Single Integer Answer Type Questions)3videos
ESSENTIAL MATHEMATICAL TOOLS
- BOOK - ARIHANT MATHSCHAPTER - GRAPHICAL TRANSFORMATIONSEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)10videos
GRAPHICAL TRANSFORMATIONS
Similar Questions
Which of the following graphs are graphs of a function?

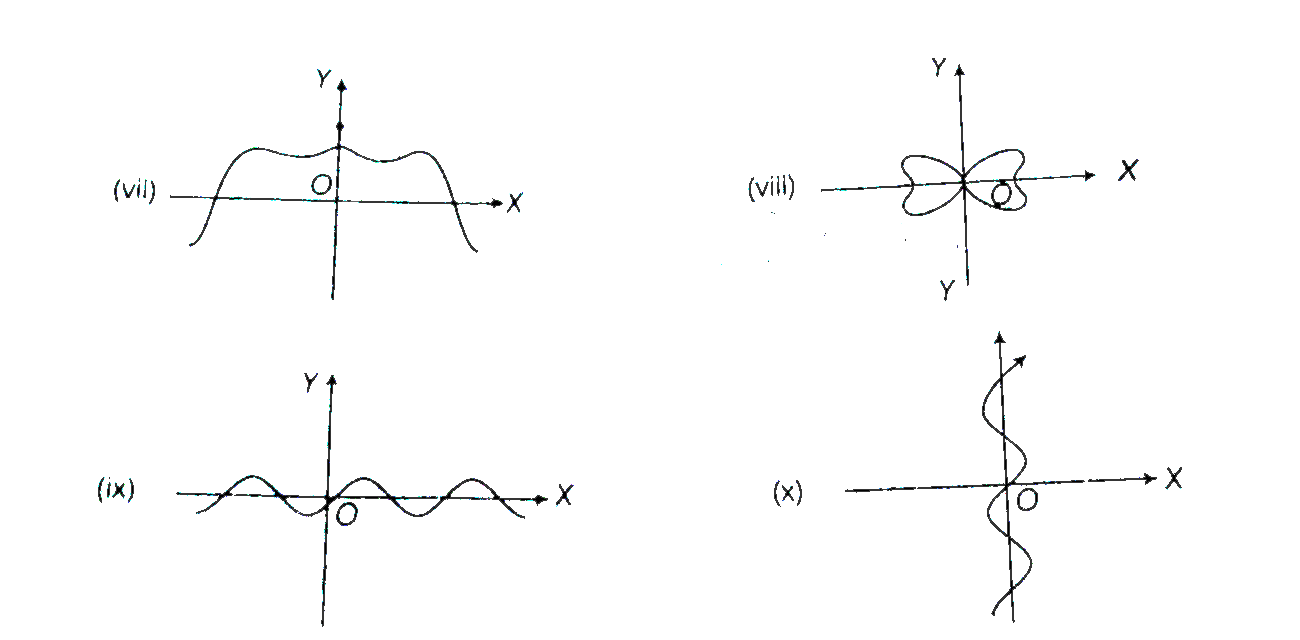 07:18View Solution
07:18View SolutionThe domain of the function
f(x)=√x2−5x+6+√2x+8−x2 , is10:08View SolutionThe number of solutions of the equation |x−1|−|2x−5|=2x
03:45View SolutionFind the number of solutions of the equation x21−|x−2|=1, graphically.
04:44View SolutionLet f(x)=max{1+sinx,1,1−cosx},x∈[0,2π],andg(x)=max{1,|x−1|},x∈R. Then (a)g(f(0))=1 (b) g(f(1))=1 (c)f(f(1))=1 (d) f(g(0))=1sin1
01:19View SolutionLet f(x)=||x|-1|-1| and g(x)-(max f(t):x<=t<=x+1,x in R} The graph of g(x) is symmetrical about
02:11View SolutionLet f(x)=max{1-x,1+x,2}. Prove that f(x) is continuous at all points but notdifferentiable at x=1 and x=-1
02:12View SolutionSometimes functions are defined like f(x)=max{sinx,cosx} , then f(x) is splitted like f(x)={{:(cosx, x in (0,(pi)/(4)]),(sinx, x in ((pi)/(4),(pi)/(2)]):} etc. If f(x)=max{(1)/(2),sinx} , then f(x)=(1)/(2) is defined when x in
02:12View SolutionLet p (x) be a polynomial with real coefficient and p(x)=x2+2x+1. Find P (1).
04:04View SolutionLet f(x)=max(1+s∈x,1,1−cosx),x∈[0,2π],andg(x)=max{1,|x−1|},x∈R. Then g(f(0))=1 (b) g(f(1))=1 f(f(1))=1 (d) f(g(0))=1+sin1
09:46View SolutionLet f(x)=sinx+cosx,g(x)=x2−1. Then g(f(x)) is invertible for x∈
04:26View SolutionLet f(x)=max{tanx, cotx}. Then the number of roots of the equation f(x)=1√3 in (0,2π) is
05:03View SolutionLet f(x) = max { 1+ sin x, 1.1 -cos x } , x in [0,2pi ] and g(x) = max {1, |x-|} x in R Then
View Solution(0,2π) में उन बिंदुओं की कुल संख्या, जहां f(x)=max.{sinx,cosx,1−cosx} अवकलनीय नहीं है बराबर है
05:27View SolutionLet f(x)=max{1+sinx,1,1−cosx},ξn[0,2π]andg(x)=max{1,|x−1|}x∈R, then
06:12View SolutionLet f(x)=max{sinx,cosx}∀x∈R then number of critical points of f(x) in (0,2π) is
02:24View Solution

