Let C be the set of curves having the property that the point of intersection of tangent with y-axis is equidistant from the point of tangency and origin (0,0)
If C1,C2∈C such that
C1: Curve is passing through (1,0)
C2: Curve is passing through (−1,0)
The number of common tangents for C1andC2 is Solution in Punjabi
1
2
3
None of these
The correct Answer is:C
Step by step video & image solution for Let C be the set of curves having the property that the point of intersection of tangent with y-axis is equidistant from the point of tangency and origin (0,0) If C_(1),C_(2) in C such that C_(1): Curve is passing through (1,0) C_(2): Curve is passing through (-1,0) The number of common tangents for C_(1) and C_(2) is by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- DIFFERENTIAL EQUATION BOOK - ARIHANT MATHSCHAPTER - DIFFERENTIAL EQUATION EXERCISE - Differential Equations Exerise 5 :
3 Videos
- DIFFERENTIAL EQUATION BOOK - ARIHANT MATHSCHAPTER - DIFFERENTIAL EQUATION EXERCISE - Exercise (Single Integer Answer Type Questions)
8 Videos
- DIFFERENTIAL EQUATION BOOK - ARIHANT MATHSCHAPTER - DIFFERENTIAL EQUATION EXERCISE - Exercise (Statement I And Ii Type Questions)
9 Videos
- DETERMINANTS BOOK - ARIHANT MATHSCHAPTER - DETERMINANTS EXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
18 Videos
- DIFFERENTIATION BOOK - ARIHANT MATHSCHAPTER - DIFFERENTIATION EXERCISE - Exercise For Session 10
4 Videos
Similar Questions
Prove that 3tan2(π6)+cosesc(π6)+2tan2(π3)=9
View SolutionFind the constant of intergration by the general solution of the differential equation (2x2y−2y4)dx+(2x3+3xy3)dy=0 if curve passes through (1,1).
View SolutionStatement I Differential equation corresponding to all lines, ax+by+c=0 has the order 3.
Statement II Gereral solution of a differential equation of nth order contains n independent arbitaray constanis.
View SolutionIf a2+b2+c2=−2, and f(x)= ∣∣ ∣ ∣∣1+a2x(1+b2)x(1+c2)x(1+a2)x1+b2x(1+c2)x(1+a2)x(1+b2)x1+c2x∣∣ ∣ ∣∣ , then f(x) is a polynomial of degree
View SolutionThe functions f(x)−ex+x, being differentiable and one-one, has a differentiable inverse f−1(x) The value of ddxf−1 at the point f(log2) is
View SolutionThe equation of a circle C1 is x2+y2=4. The locus of the intersection of orthogonal tangents to the circle is the curve C2 and the locus of the intersection of perpendicular tangents to the curve C2 is the curve C3, Then
View SolutionA curve C passes through origin and has the property that at each point (x,y) on it the normal line at that point passes through (1,0) The equation of a common tangent to the curve C and the parabola y^(2)=4x is
View SolutionFrom the point A, common tangents are drawn to the curve C_(1):x^(2)+y^(2)=8 and C_(2):y^(2)=16x. The y- intercept of common tangent between C_(1) and C_(2) having negative gradients,is
View SolutionThe equation of a circle is x^(2)+y^(2)+14x-4y+28=0. The locus of the point of intersection of orthoonal tangents to C_(1) is the curve C_(2) and the locus of the point of intersection of perpendicular tangents to C_(2) is the curve C_(3) then the statement(s) which hold good?
View SolutionThe centres of two circles C1andC2 each of unit radius are at a distance of 6 unit from each other. Let P be the mid-point of the line segment joining the centres of C1andC2 and C be a circle touching circles C1andC2 externally. If a common tangent to C1 and C passing through P is also a common tangent to C2 and C, then the radius of the circle C, is
View SolutionLet C be the set of curves having the property that the point of intersection of tangent with y-axis is equidistant from the point of tangency and origin (0,0)
If C3∈C
C3: is passing through (2,4). If xa+yb=1. is tangent to C3, then
View SolutionLet C be the set of curves having the property that the point of intersection of tangent with y-axis is equidistant from the point of tangency and origin (0,0)
If common tangents of C1andC2 form an equilateral triangle, where C_(1),C_(2) in C and C_(1):Curvepassesthroughf(2,0),thenC_(2) may passes through
View SolutionLet C1andC2 be two curves passing through the origin as shown in the figure. A curve C is said to ‘‘bisect the area’’ the region between C1andC2, if for each point P of C, the two shaded regions A and B shown in the figure have equal areas. Determine the upper curve C2, given that the bisecting curve C has the equationy=x2 and that the lower curve C1 has the equation y=x2/2.
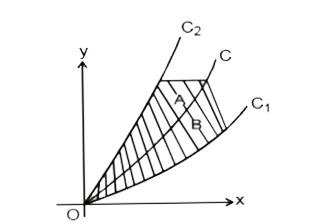
View SolutionConsider the curve C1:x2−y2=1 and C2:y2=4x then ,The number of lines which are normal to C2 and tangent to C1 is
View SolutionConsider the curve C1:x2−y2=1 and C2:y2=4x then The point of intersection of directrix of the curve C2 with C1
View SolutionNews C_(1) Equation of x^(2) + y^(2) = 4 Is The curve of intersection of the perpendicular tangents drawn on the circle C_(2) Is and curve C_(2) The curve of intersection of the perpendicular tangent drawn on C_(3) Is then
View Solution
