If A,B,C are the angles of a triangle then prove that cosA+cosB−cosC=−1+4cos(A2)cos(B2)sin(C2)Solution in Punjabi
The correct Answer is:cosA+cosB+cosC=1+rR
Step by step video & image solution for If A,B,C are the angles of a triangle then prove that cosA+cosB-cosC=-1+4cos(A/2)cos(B/2)sin(C/2) by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- PROPERTIES AND SOLUTION OF TRIANGLES BOOK - ARIHANT MATHSCHAPTER - PROPERTIES AND SOLUTION OF TRIANGLES EXERCISE - SOLVED EXAMPLES
1 Videos
- PROPERTIES AND SOLUTION OF TRIANGLES BOOK - ARIHANT MATHSCHAPTER - PROPERTIES AND SOLUTION OF TRIANGLES EXERCISE - Exercise For Sesssion 1
20 Videos
- PRODUCT OF VECTORSBOOK - ARIHANT MATHSCHAPTER - PRODUCT OF VECTORSEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
52 Videos
- SEQUENCES AND SERIESBOOK - ARIHANT MATHSCHAPTER - SEQUENCES AND SERIESEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
38 Videos
Similar Questions
Match the statements of Column I with values of Column II.

View SolutionIn the given figure,if AB=AC,∠BAD=30∘andAE=AD, then x is equal to
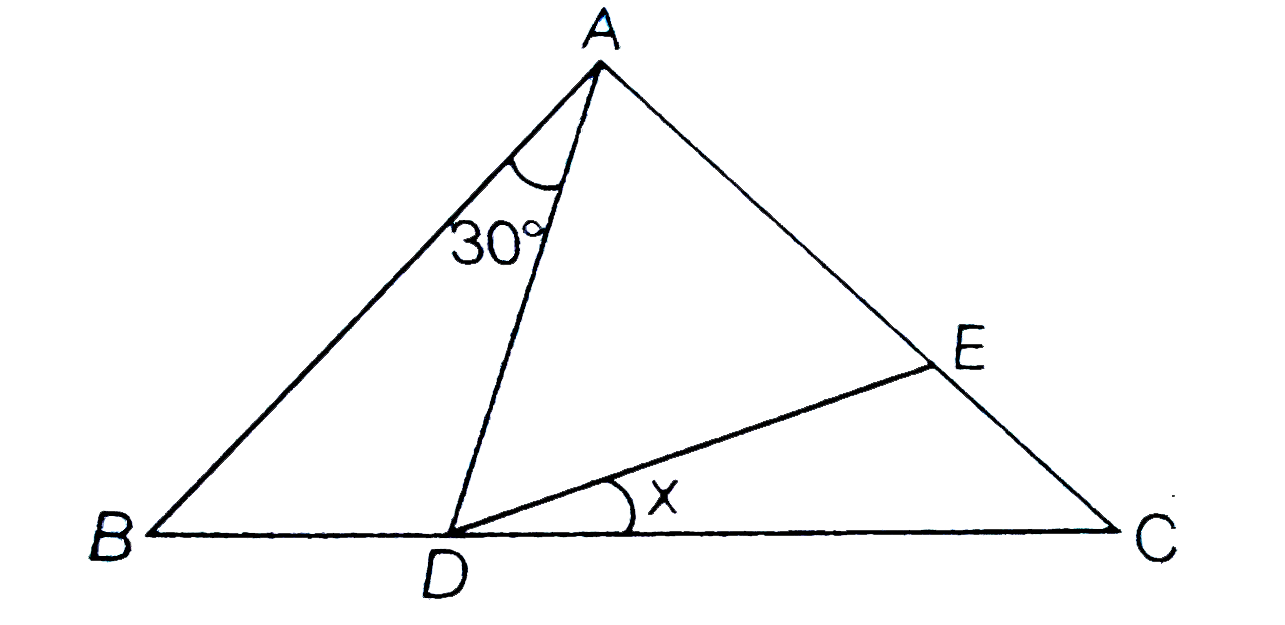
View SolutionLet O be the origin and let PQR be an arbitrary triangle. The point S is such that ¯¯¯¯¯¯OP⋅¯¯¯¯¯¯OQ+¯¯¯¯¯¯OR⋅¯¯¯¯¯¯OS=¯¯¯¯¯¯OR⋅¯¯¯¯¯¯OP+¯¯¯¯¯¯OQ⋅¯¯¯¯¯¯OS=¯¯¯¯¯¯OQ⋅¯¯¯¯¯¯OR+¯¯¯¯¯¯OP⋅¯¯¯¯¯¯OS Then the triangle PQR has S as its
View SolutionLet a,b,c be in A.P. and |a|<1,|b|<1|c|<1.ifx=1+a+a2+....to ∞,y=1+b+b2+....to ∞and,z=1+c+c2+...to ∞, then x,y,z are in
View SolutionIf A+B+C=π, prove that : cosA+cosB−cosC=4cos(A2)cos(B2)sin(C2)−1
View SolutionIf A,B and C are angles of a triangle then the determinant
∣∣ ∣∣−1cosCcosBcosC−1cosAcosBcosA−1∣∣ ∣∣ is equal to
View SolutionIf A,B,C be anlges of a triangle, then prove that, ∣∣ ∣∣−1cosCcosBcosC−1cosAcosBcosA−1∣∣ ∣∣=0
View Solutionयदि A+B+C=π हो तो सिद्ध कीजिए कि -
1+cosA−cosB+cosC1+cosA+cosB−cosC=tanB2cotC2.
View SolutionIf A,B,C are angles in a triangle , then prove that cosA+cosB+cosC=1+4sin.A2sin.B2sin.C2
View SolutionIF A,B,C are angles in the triangle, then prove that
cosA+cosB−cosC=−1+4cosA2.cosB2.sinC2
View Solutionदर्शाइए कि त्रिभुज ABC एक समद्विबाहु त्रिभुज है यदि सारणिक :
Δ=⎡⎢⎣1111+cosA1+cosB1+cosCcos2A+cosAcos2B+cosBcos2C+cosC⎤⎥⎦=0
View Solutionयदि A, B और C एक त्रिभुज के कोण हैं तो सारणिक ∣∣ ∣∣1cosCcosBcosC1cosAcosBcosA1∣∣ ∣∣ बराबर है :
View SolutionIf A,B,C are the angles of a triangles then Δ=∣∣ ∣∣−1cosCcosBcosC−1cosAcosBcosA−1∣∣ ∣∣=
View SolutionProve that cosA−cosB−cosC=1−4sin(A2)cos(B2)cos(C2),if A+B+C=π
View SolutionProve it (b^2-c^2)/(cosB+cosC)+(c^2-a^2)/(cosC+cosA)+(a^2-b^2)/(cosA+cosB)=0
View SolutionIf A,B,C are interior angles of a triangle ABC such that (cosA+cosB+cosC)2+(sinA+sinB+sinC)2=9 then the number of possible triangle is
View Solution
