Each side of an equilateral triangle subtends an angle of 60∘ at the top of a tower h m high located at the centre of the triangle. If a is the length of each side of the triangle, then Solution in Punjabi
3a2=2h2
2a2=2h2
a2=3h2
3a2=h2
The correct Answer is:A, B, C
Step by step video & image solution for Each side of an equilateral triangle subtends an angle of 60^(@) at the top of a tower h m high located at the centre of the triangle. If a is the length of each side of the triangle, then by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- PROPERTIES AND SOLUTION OF TRIANGLES BOOK - ARIHANT MATHSCHAPTER - PROPERTIES AND SOLUTION OF TRIANGLES EXERCISE - SOLVED EXAMPLES
1 Videos
- PROPERTIES AND SOLUTION OF TRIANGLES BOOK - ARIHANT MATHSCHAPTER - PROPERTIES AND SOLUTION OF TRIANGLES EXERCISE - Exercise For Sesssion 1
20 Videos
- PRODUCT OF VECTORSBOOK - ARIHANT MATHSCHAPTER - PRODUCT OF VECTORSEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
52 Videos
- SEQUENCES AND SERIESBOOK - ARIHANT MATHSCHAPTER - SEQUENCES AND SERIESEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
38 Videos
Similar Questions
Match the statements of Column I with values of Column II.

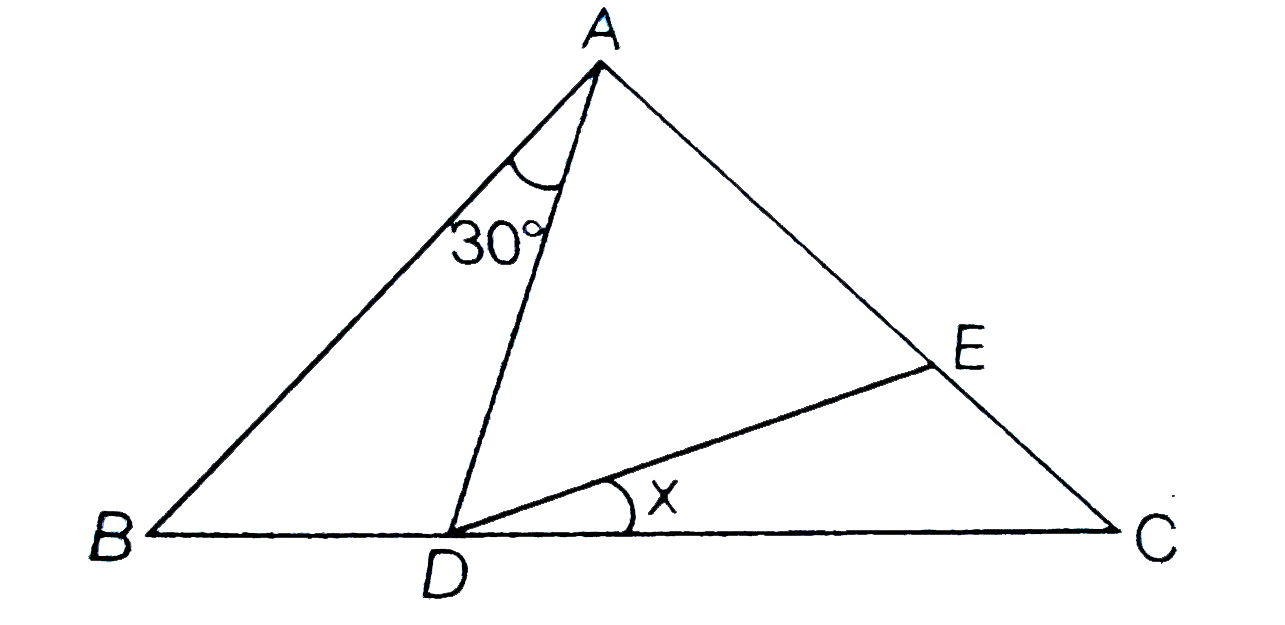
View SolutionIn the given figure,if AB=AC,∠BAD=30∘andAE=AD, then x is equal to
View SolutionLet O be the origin and let PQR be an arbitrary triangle. The point S is such that ¯¯¯¯¯¯OP⋅¯¯¯¯¯¯OQ+¯¯¯¯¯¯OR⋅¯¯¯¯¯¯OS=¯¯¯¯¯¯OR⋅¯¯¯¯¯¯OP+¯¯¯¯¯¯OQ⋅¯¯¯¯¯¯OS=¯¯¯¯¯¯OQ⋅¯¯¯¯¯¯OR+¯¯¯¯¯¯OP⋅¯¯¯¯¯¯OS Then the triangle PQR has S as its
View SolutionLet a,b,c be in A.P. and |a|<1,|b|<1|c|<1.ifx=1+a+a2+....to ∞,y=1+b+b2+....to ∞and,z=1+c+c2+...to ∞, then x,y,z are in
View SolutionEach side of an equilateral triangle subtends angle of 60^(@) at the top of a tower of height h stand centre of the triangle.If 2a be the length of the side of the triangle,then (a^(2))/(h^(2))=
View SolutionEach side of a square ABCD subtends an angle of 60^(@) at the top of a tower of height h standing at the centre of a square.If a be the length of the side of the square,then
View SolutionEach side of a square substends an angle of 60^@ at the top of a tower h metres h metres high standing in the centre of the square . If a is the length of each side of the square , then
View SolutionIf the sides of an equilateral triangle be increased by 2 cm each, the area of the triangle is increased by 2√3cm2. Determine the length of each sides of the equilateral triangle.
View SolutionEach side of the equilateral triangle shown is 2. What is the height h of the triangle?
View SolutionA 10 meters high tower is standing at the centre of an equilateral triangle and each side of the triangle subtends an angle of 60∘ at the top of the tower. Then the length of each side of the triangle is.
View SolutionA 10 meters high tower is standing at the center of an equilateral triangel and each side of the triangle subtends an angle of 60∘ at the top of the tower. Then the lengthof each side of the triangel is
View Solutionसमबाहु त्रिभुज में प्रत्येक भुजा होती है -
View SolutionA flagstaff 10 m high stands at the centre of a equilateral triangle, which is horizontal. At the top of the flagstaff each side subtends at an angle of 60°. The length of each side of the triangle is
View SolutionIf each side of length a of an equilateral triangle subtends an angle of 60∘ at the top of a tower h meter high situated at the centre of the triangle, then
View SolutionIf each side of length 'a' of an equilateral triangle subteds an angle of 60∘ at the top of a tower h metrs eigh situated at the centre of the triangle , then
View SolutionIf each side of length 'a' of an equilateral triangle substends an angle of 60∘ at the top of a tower h metrs heigh situated at the centre of the triangle then
View Solution
