The base of a triangle is divided into three equal parts. If t1,t2,t3 are the tangents of the angles subtended by these parts at the opposite vertex, prove that (1t1+1t2)(1t2+1t3)=4(1+1(t2)2)).Solution in Punjabi
The correct Answer is:4(1+1t22)=(1t1+1t1)(1t2+1t2)
Step by step video & image solution for The base of a triangle is divided into three equal parts. If t_1, t_2,t_3 are the tangents of the angles subtended by these parts at the opposite vertex, prove that (1/(t_1)+1/(t_2))(1/(t_2)+1/(t_3))=4(1+1/(t_2)^ 2))dot by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- PROPERTIES AND SOLUTION OF TRIANGLES Book:ARIHANT MATHSChapter:PROPERTIES AND SOLUTION OF TRIANGLES Exercise:SOLVED EXAMPLES
Explore 1 Video
- PROPERTIES AND SOLUTION OF TRIANGLES Book:ARIHANT MATHSChapter:PROPERTIES AND SOLUTION OF TRIANGLES Exercise:Exercise For Sesssion 1
Explore 20 Videos
- PRODUCT OF VECTORSBook:ARIHANT MATHSChapter:PRODUCT OF VECTORSExercise:Exercise (Questions Asked In Previous 13 Years Exam)
Explore 52 Videos
- SEQUENCES AND SERIESBook:ARIHANT MATHSChapter:SEQUENCES AND SERIESExercise:Exercise (Questions Asked In Previous 13 Years Exam)
Explore 38 Videos
Similar Questions
Match the statements of Column I with values of Column II.

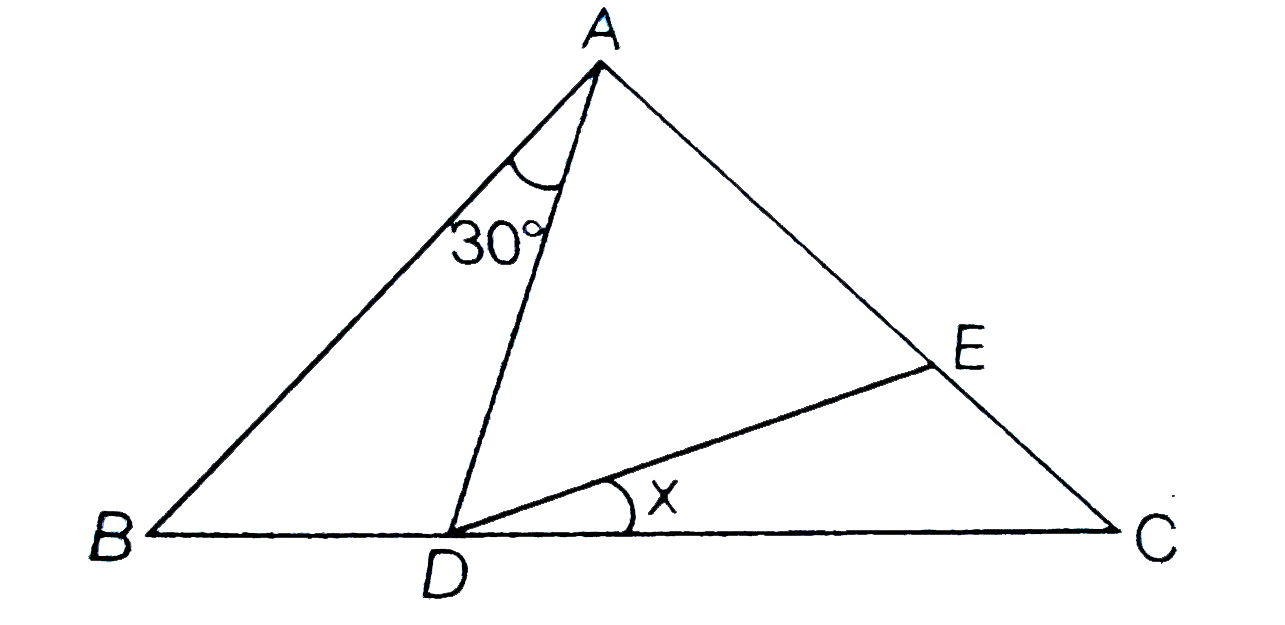
View SolutionIn the given figure,if AB=AC,∠BAD=30∘andAE=AD, then x is equal to
View SolutionLet O be the origin and let PQR be an arbitrary triangle. The point S is such that ¯¯¯¯¯¯OP⋅¯¯¯¯¯¯OQ+¯¯¯¯¯¯OR⋅¯¯¯¯¯¯OS=¯¯¯¯¯¯OR⋅¯¯¯¯¯¯OP+¯¯¯¯¯¯OQ⋅¯¯¯¯¯¯OS=¯¯¯¯¯¯OQ⋅¯¯¯¯¯¯OR+¯¯¯¯¯¯OP⋅¯¯¯¯¯¯OS Then the triangle PQR has S as its
View SolutionLet a,b,c be in A.P. and |a|<1,|b|<1|c|<1.ifx=1+a+a2+....to ∞,y=1+b+b2+....to ∞and,z=1+c+c2+...to ∞, then x,y,z are in
View Solutiont1=(sinθ)cosθ,t2=(sinθ)sinθ,t3=(cosθ)cosθ,t4=(cosθ)sinθ (A) t3>t1>t2 (B) t4>t2>t1 (C) t4>t1>t2 (D) t1>t3>t2
View SolutionThe vertices of a triangle are [a t_1t_2,a(t_1 +t_2)], [a t_2t_3,a(t_2 +t_3)], [a t_3t_1,a(t_3 +t_1)] Then the orthocenter of the triangle is (a) (-a, a(t_1+t_2+t_3)-at_1t_2t_3) (b) (-a, a(t_1+t_2+t_3)+at_1t_2t_3) (c) (a, a(t_1+t_2+t_3)+at_1t_2t_3) (d) (a, a(t_1+t_2+t_3)-at_1t_2t_3)
View SolutionAssertion (A) : Orthocentre of the triangle formed by any three tangents to the parabola lies on the directrix of the parabola
Reason ® : The orthocentre of the triangle formed by the tangents at t1,t2,t3 to the parabola y2=4axis(−a(t1+t2+t3+t1t2t3))
View SolutionThe vertices of a triangle are [at1t2,a(t1+t2)], [at2t3,a(t2+t3)], [at3t1,a(t3+t1)] Then the orthocenter of the triangle is (a) (−a,a(t1+t2+t3)−at1t2t3) (b) (−a,a(t1+t2+t3)+at1t2t3) (c) (a,a(t1+t2+t3)+at1t2t3) (d) (a,a(t1+t2+t3)−at1t2t3)
View SolutionThe vertices of a triangle are [at1t2,a(t1+t2)], [at2t3,a(t2+t3)], [at3t1,a(t3+t1)] Then the orthocenter of the triangle is: (a) (−a,a(t1+t2+t3)−at1t2t3) (b) (−a,a(t1+t2+t3)+a(t1t2t3) (c) (a,a(t1+t2+t3)+at1t2t3) (d) (a,a(t1+t2+t3)−at1t2t3)
View SolutionWrite the correct number in the given blanks from the following A.P.1,8,15,22. a=... t1=....,t2=....,t3=.... t2−t1=....andt3−t2=...., hence d=....
View SolutionWrite the correct number in the given blanks from the following A.P.3,6,9,12. a=... t1=....,t2=....,t3=.... t2−t1=....andt3−t2=...., hence d=....
View SolutionWrite the correct number in the given blanks from the following A.P.70,60,50,40. a=... t1=....,t2=....,t3=.... t2−t1=....andt3−t2=...., hence d=....
View SolutionShow that the relation R. defined in the set A of all triangle as R={(T1,T2):T1is similar to T2,is an equivalence relation. Consider three right angled triangles T1with sides 3,4,5,T2 with sides 5,12,13 and T3 with sides 6,8,10. Which triangle among T1,T2 andT3 are related ?
View SolutionIf t1,t2 and t3 are distinct, the points (t1,2at1+at31),(t2,2at2+at32),(t3,2at3+at33) are collinear then show that t1+t2+t3=0.
View SolutionThe vertices of a triangle are
[at1t2,a(t1+t2)],[at2t3,a(t2+t3)],[at3t1,a(t3+t1)]
Find the orthocentre of the triangle.
View SolutionArea of the triangle formed by the threepoints 't1'.'t2'and't3' on y2=4ax is K|(t1−t2)(t2−t3)(t3−t1)| then K=
View Solution