The coefficient of (x3⋅b6⋅C8⋅d9⋅e⋅f) in the expansion
of (a+b+c−d−e−f)31 is Solution in Punjabi
12632
23110
3110
None of these
The correct Answer is:d
Coefficient of (a3⋅b6⋅c8⋅d9⋅e⋅f) in given expansion
=(−1)9⋅(−1)1⋅(−1)1⋅31!316!8!9!1!1!
Topper's Solved these Questions
- BIONOMIAL THEOREMBOOK - ARIHANT MATHSCHAPTER - BIONOMIAL THEOREMEXERCISE - Exercise (More Than One Correct Option Type Questions)
15 Videos
- BIONOMIAL THEOREMBOOK - ARIHANT MATHSCHAPTER - BIONOMIAL THEOREMEXERCISE - Exercise (Passage Based Questions)
21 Videos
- BIONOMIAL THEOREMBOOK - ARIHANT MATHSCHAPTER - BIONOMIAL THEOREMEXERCISE - Exercise For Session 4
14 Videos
- AREA OF BOUNDED REGIONSBOOK - ARIHANT MATHSCHAPTER - AREA OF BOUNDED REGIONSEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
23 Videos
- CIRCLE BOOK - ARIHANT MATHSCHAPTER - CIRCLE EXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
16 Videos
Similar Questions
If in the expansion of (1+x)m(1−x)n , the coefficients
of x and x2 are 3 and - 6 respectively, the value of m and n are
View SolutionFind the value of x if |3−4i|=5x
View SolutionThe coefficient of a8b4c9d9 in (abc+abd+acdd+bcd)10 is 10! b. 10!8!4!9!9! c. 2520 d. none of these
View SolutionArea of the region
{(x,y)∈R2:y≥√|x+3|,5y≤x+9≤15} is equal to
View SolutionFind the derivative of (ax4−bx2+cosx)
View SolutionIf ABC and DEF are two triangles such that ABDE=BCEF=CAFD=25 , then Area(ABC):Area(DEF)= 2:5 (b) 4:25 (c) 4:15 (d) 8:125
View SolutionIf in two triangles ABC and DEF , ABDE=BCFE=CAFD , then FDECAB (b) FDEABC (c) CBAFDE (d) BCAFDE
View SolutionD, E, F are the mid-point of the sides BC, CA and AB respectively of ABC. Then DEF is congruent to triangle. ABC (b) AEF (c) BFD, CDE (d) AFE, BFD, CDE
Given : D, E, F are the mid-point of the sides BC, CA and AB .
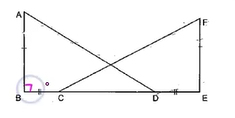
View SolutionIn Figure, AB⊥BEandFE⊥BE.If BC=DEandAB=EF, then ABD is congruent to:
(a)EFC
(b) ECF
(c) CEF
(d) FEC
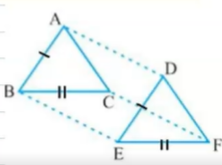
View SolutionIf ABC and DEF are two triangles such that AB, BC are respectively equal and parallel to DE, EF, then show that Quadrilateral ABED is a parallelogram Quadrilateral BCFE is a parallelogram AC=DF (iv) ABC ≅ DEF
View SolutionVerify: (ab+cd)+ef=ab+(cd+ef)f or ab= −23,cd=57 a n d ef=−16.
View SolutionIf ab=cd=ef, then a3+c3+e3b3+d3+f3=___
View Solutiona d c e b e d f e h e ?
View SolutionThe coefficient of (x3⋅b6⋅C8⋅d9⋅e⋅f) in the expansion
of (a+b+c−d−e−f)31 is
View SolutionIf ab=bc=cd=de=ef=13, find the value of (a+b+c+d+eb+c+d+e+f):
View SolutionIn Figure, DE∣∣AC and DF∣∣AE . Prove that EFBF=ECBE .
View Solution
