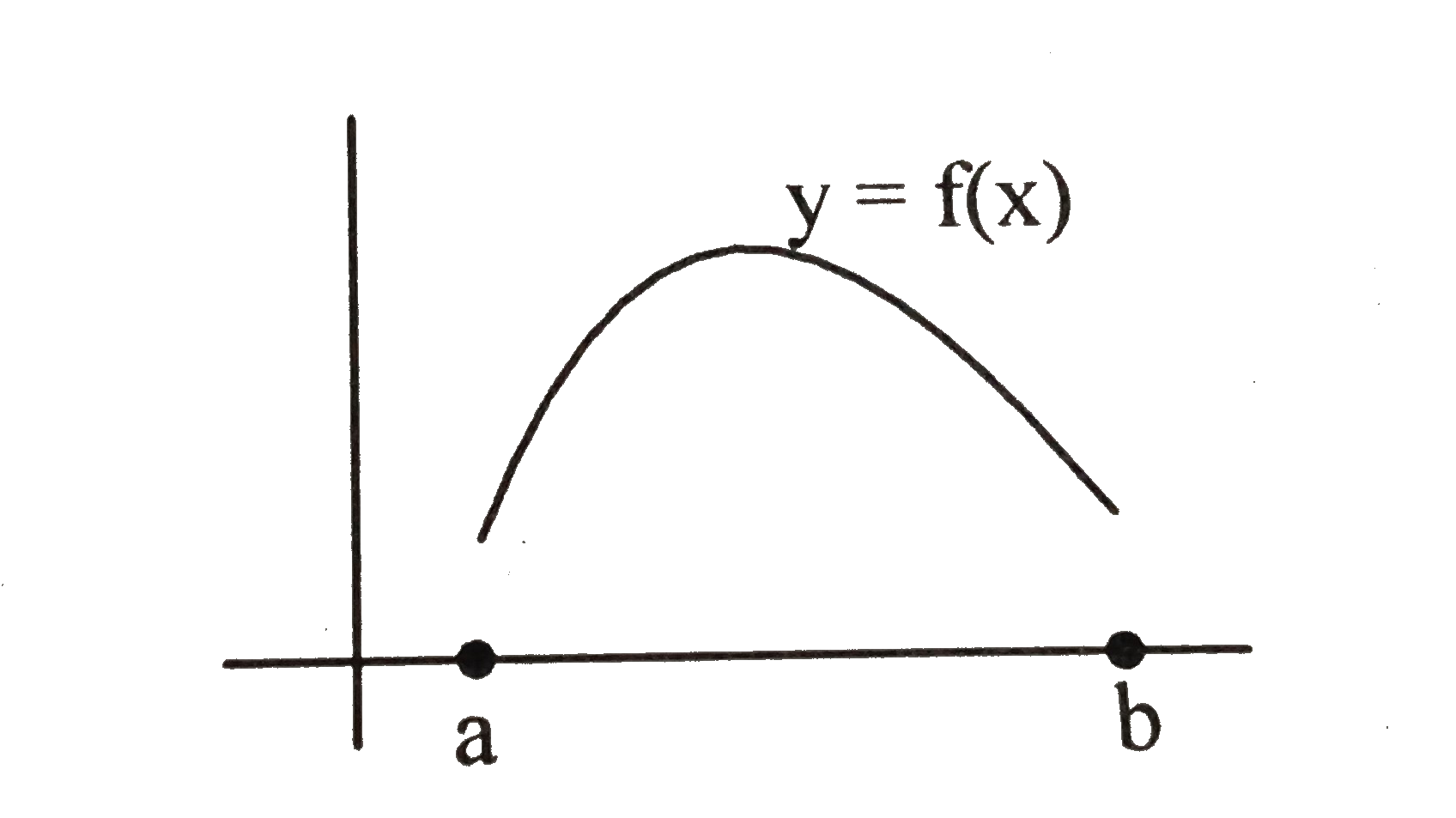
If a function (continuos and twice differentiable) is always concave upward in an interval, then its graph lies always below the segment joining extremities of the graph in that interval and vice-versa.
Let f:R+→R+ is such that f(x)≥0∀x∈[a,b]. Then value of ∫baf(x)dx cannot exceed:Solution in Punjabi
(f(a)+f(b))(b−a)3
(f(b)−f(a))(b−a)2
(f(b)+f(a))(b−a)2
None of the above
Step by step video & image solution for If a function (continuos and twice differentiable) is always concave upward in an interval, then its graph lies always below the segment joining extremities of the graph in that interval and vice-versa. Let f:R^(+)toR^(+) is such that f"(x)ge0 AAx in [a,b]. Then value of int_(a)^(b)f(x) dx cannot exceed: by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- MONOTONICITY MAXIMA AND MINIMABook:ARIHANT MATHSChapter:MONOTONICITY MAXIMA AND MINIMAExercise:Exercise For Session 1
Explore 7 Videos
- MONOTONICITY MAXIMA AND MINIMABook:ARIHANT MATHSChapter:MONOTONICITY MAXIMA AND MINIMAExercise:Exercise For Session 2
Explore 4 Videos
- MONOTONICITY MAXIMA AND MINIMABook:ARIHANT MATHSChapter:MONOTONICITY MAXIMA AND MINIMAExercise:Exercise (Questions Asked In Previous 13 Years Exam)
Explore 31 Videos
- MATRICES Book:ARIHANT MATHSChapter:MATRICES Exercise:Exercise (Questions Asked In Previous 13 Years Exam)
Explore 49 Videos
- PAIR OF STRAIGHT LINES Book:ARIHANT MATHSChapter:PAIR OF STRAIGHT LINES Exercise:Exercise (Questions Asked In Previous 13 Years Exam)
Explore 2 Videos
Similar Questions
Evaluate n!(n−r)! , when n = 7 , r = 4
View SolutionDetermine all the critical points for the function f(x)=6x5+33x4−30x3+100
View SolutionThe least value of α∈R for which 4ax2+1x≥1, for all x>0, is
View SolutionLet A=⎡⎢⎣1000110−24⎤⎥⎦,I=⎡⎢⎣100010001⎤⎥⎦andA−1=[16(A2+cA+dI)] Then value of candd are (a) (−6,−11) (b) (6,11) (c) (−6,11) (d) (6,−11)
View SolutionIf the pair of lines ax2+2(a+b)xy+by2=0 lie along diameters of a circle and divide the circle into four sectors such that the area of one of the sectors is thrice the area of another sector then
View SolutionThe graph of the derivative f of a continuous function fis~ shown with f(0)=0, then for f(x) find (i) Intervals of monotonicity (ii) Intervals of concavity
View SolutionLet f:R rarr R be a differentiable function such that f(a)=0=f(b) and f'(a)f'(b)>0 for some a
View SolutionThe following figure shows the graphs of a differentiable fucntion y=f(x) on the interval [a,b] (not contaning 0).
Let g(x)=f(x)/x which of the following is a possible graph of y=g(x) ?
View SolutionIf f(x) is double differentiable function such that |f"(x)|le5 for each x in the interval [0,4] and f takes its largest value at an interior point of this interval , then value of |f'(0)|+|f,'(4)| cannot be -
View SolutionLet f:R→R be a function defined by f(x)=|x|3+|x|1+x2, then the graph of f(x) lies in the
View SolutionLet f(x) be a differentiable function in the interval (0, 2) then the value of ∫20f(x)dx
View SolutionLet f:[a,b]→R be such that f is differentiable in (a,b), f is continuous at x=a and x=b and moreover f(a)=0f(b). Then
View SolutionLet f(x) be a differentiable function in the interval (0,2) then the value of ∫20f(x) is
View SolutionLet the function, f:[−7,0]→R be continuous on [−7,0] and differentiable on (−7,0). If f(−7)=−3 and f'(x)≤2, for all x∈(−7,0), then for all such functions f,f(−1)+f(0) lies in the interval :
View SolutionProceeding from geometric reasoning, prove that :
(a) if the function f(x) increases and has a concave graph in the interval [a,b], then
(b,a)f(a)<∫baf(x)dx<(b−a)f(a)+f(b)2
(b) if the function f(x) increases and has a convex graph in the interval [a,b], then
(b−a)f(a)+f(b)2<∫baf(x)dx<(b−a)f(b)
View SolutionLet f(x) be a differentiable function in the interval (0,2) , then the value of ∫20f(x)dx is :
View Solution