Let f:(0,∞)→→R
be given by f(x)=∫x1xe−(t+1t)dtt,
then
Solution in Punjabi
(a) f(x) is monotonically increasing on [1,∞)
(b) f(x) is monotonically decreasing on [0,1]
(c) f(x)+f(1x)=0,∀x∈(0,∞)
(d) f(2x) is an odd function pf x on R
The correct Answer is:C
Step by step video & image solution for Let f:(0,oo) to vec R be given by f(x)=int_(1/x)^x(e^(-(t+1/t))dt)/t , then by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- MONOTONICITY MAXIMA AND MINIMABook:ARIHANT MATHSChapter:MONOTONICITY MAXIMA AND MINIMAExercise:MAXIMA AND MINIMA EXERCISE 6
Explore 2 Videos
- MATRICES Book:ARIHANT MATHSChapter:MATRICES Exercise:Exercise (Questions Asked In Previous 13 Years Exam)
Explore 49 Videos
- PAIR OF STRAIGHT LINES Book:ARIHANT MATHSChapter:PAIR OF STRAIGHT LINES Exercise:Exercise (Questions Asked In Previous 13 Years Exam)
Explore 2 Videos
Similar Questions
The figure shows a right triangle with its hypotenuse OB along the y-axis and its vertex A on the parabola y=x2.
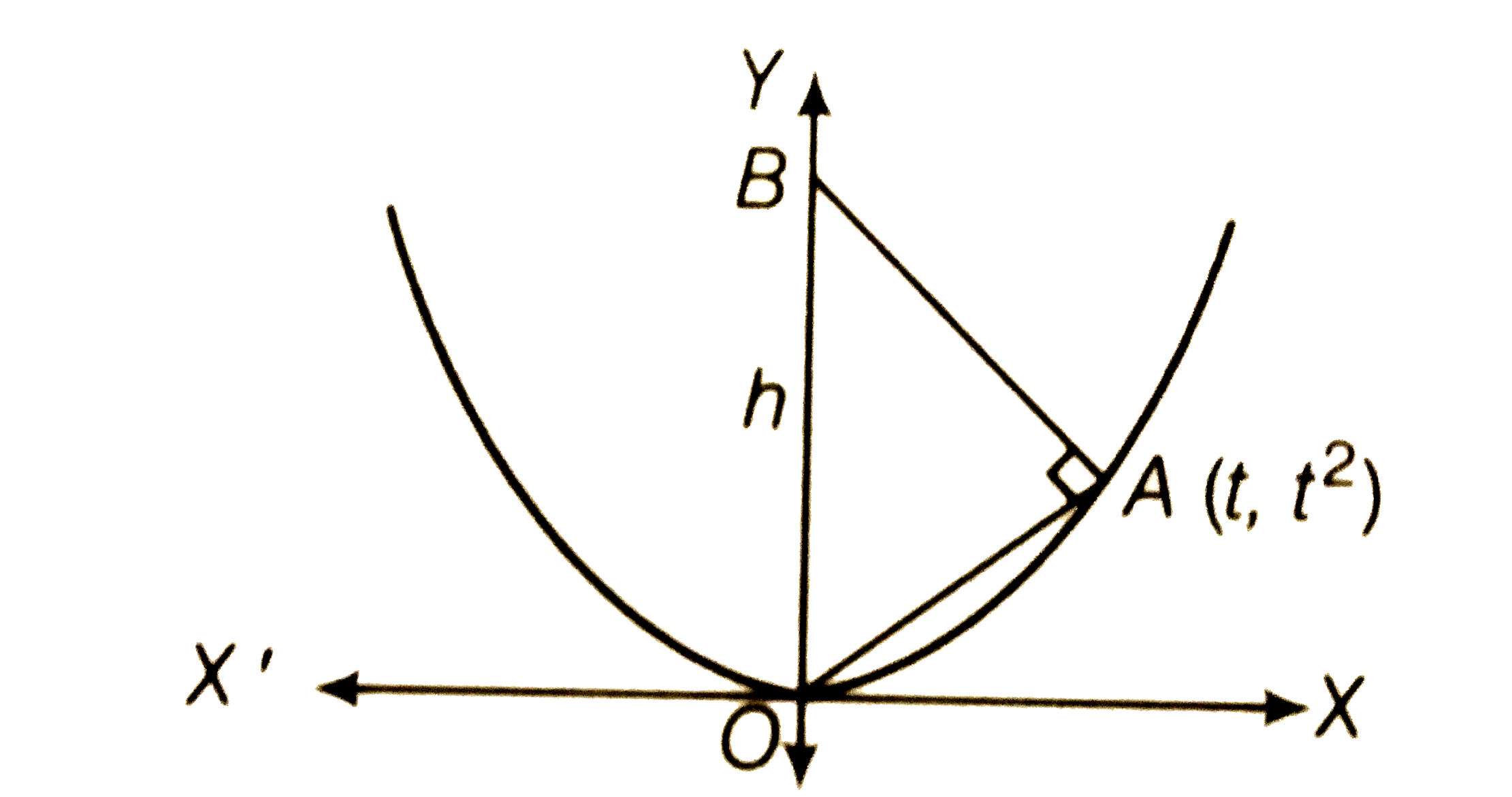
Let h represents the length of the hypotenuse which depends on the x-coordinate of the point A. The value of limt→o(h) is equal to
View SolutionLet A=⎡⎢⎣1000110−24⎤⎥⎦,I=⎡⎢⎣100010001⎤⎥⎦andA−1=[16(A2+cA+dI)] Then value of candd are (a) (−6,−11) (b) (6,11) (c) (−6,11) (d) (6,−11)
View SolutionIf the pair of lines ax2+2(a+b)xy+by2=0 lie along diameters of a circle and divide the circle into four sectors such that the area of one of the sectors is thrice the area of another sector then
View SolutionLet f:(0,∞)→R be given by f(x)=∫x1xe−(t+1t)dtt, then (a)f(x) is monotonically increasing on [1,∞) (b)f(x) is monotonically decreasing on (0,1) (c)f(2x) is an odd function of x on R
View SolutionIf int_(0)^(x)f(t)dt=x+int_(x)^(1)f(t)dt ,then the value of f(1) is
View SolutionLet f(x)=∫x0ettdt(x>0),
then e−a[f(x+1)−f(1+a)]=
View SolutionIf ∫x0f(t)dt=ex−ae2x∫10f(t)e−tdt, then
View SolutionLet f:(0,∞)∈R be given
f(x)=∫x1/xe−(t+1t)1tdt, then
View SolutionLet f(x)=∫x0et(t−1)(t−2)dt. Then, f decreases in the interval
View SolutionLet, f:(0,∞)→R be given by
f(x)=∫x1xe−(t+1t)dtt
Then
View SolutionLet f be a continuous function on (0,∞) and satisfying f(x)=(logex)2−∫e1f(t)tdt for all x≥1, then f(e) equals
View Solutionमाना f:(0,∞)→R निम्न के द्वारा f(x)=∫x1xe−(t+1t)dttपरिभाषित है | तब,
View SolutionIf ∫x0f(t)dt=x+∫1xtf(t)dt, then the value of f(1) is
View SolutionLet f:(0,∞)→R be given by f(x)=∫x1xe−(t+1t)dtt, then (a)f(x) is monotonically increasing on [1,∞) (b)f(x) is monotonically decreasing on (0,1) (c)f(2x) is an odd function of x on R (d) none of these.
View SolutionLet f(x)=∫x0ettdt(x>0),
then e−a[f(x+1)−f(1+a)]=
View SolutionIf ∫x0f(t)dt=ex−ae2x∫10f(t)e−tdt, then
View Solution