Statement I Integral of an even function is not always an odd function. Statement II Integral of an odd function is an even function .Solution in Punjabi
Statement I is true, Statement II is also true , Statement II is the correct explanation of Statement I.
Statement I is true, Statement II is also true, Statement II is not the correct explanation of Statement I.
Statement I is true, Statement II is false.
Statement I is false, Statement II is true .
The correct Answer is:C
Step by step video & image solution for Statement I Integral of an even function is not always an odd function. Statement II Integral of an odd function is an even function . by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- INDEFINITE INTEGRAL BOOK - ARIHANT MATHSCHAPTER - INDEFINITE INTEGRAL EXERCISE - Exercise (Passage Based Questions)
11 Videos
- INDEFINITE INTEGRAL BOOK - ARIHANT MATHSCHAPTER - INDEFINITE INTEGRAL EXERCISE - Exercise 5 ( Matching Type Questions )
2 Videos
- INDEFINITE INTEGRAL BOOK - ARIHANT MATHSCHAPTER - INDEFINITE INTEGRAL EXERCISE - Exercise (More Than One Correct Option Type Questions)
5 Videos
- HYPERBOLABOOK - ARIHANT MATHSCHAPTER - HYPERBOLAEXERCISE - Hyperbola Exercise 11 : Questions Asked in Previous 13 Years Exams
3 Videos
- INVERSE TRIGONOMETRIC FUNCTIONSBOOK - ARIHANT MATHSCHAPTER - INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
8 Videos
Similar Questions
If ∫f(x)cosxdx=12f2(x)+C, then f(x) can be
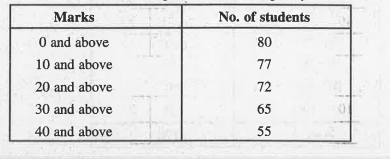
View SolutionFind the mean marks of the following cummulative frequency table :

View SolutionFind: ∫dx(x+1)(x+2)
View Solutionwhich term of the following sequence : 312,3,332.....is 81?
View SolutionIf α=3sin−1(611andβ=3cos−1(49), where the inverse trigonometric functions take only the principal values, then the correct options (s) is (are)
View SolutionThe derivative of an even function is always an odd function.
View SolutionStatement 1: If f(x) is an odd function, then f′(x) is an even function. Statement 2: If f′(x) is an even function, then f(x) is an odd function.
View SolutionProve that the derivative of an even function is an odd function and that of an odd function is an even function.
View SolutionDefinite Integration Of Odd And Even Functions
View Solutionएक विषम फलन का अवकलज सदैव एक सम फलन होता है-
View Solutionनिम्नलिखित कथनो पर विचार कीजिए
I. यदि f(x) विषम फलन है तब f'(x) सम फलन होगा
II. यदि f'(x) सम फलन है तब f(x) विषम फलन होगा
View SolutionStatement - I : If f(x) is an odd function, then f'(x) is an even function.
Statement - II : If f'(x) is an even function, then f(x) is an odd function.
View SolutionStatement I Integral of an even function is not always an odd function. Statement II Integral of an odd function is an even function .
View SolutionStatement -1 : Integral of an even function is not always on odd function.
Statement-2: Integral of an odd function is an even function.
View SolutionThe product of an odd function and an even function is:
View Solutionएक सम फलन का अवकलन सदैव एक विषम फलन होता है |
View Solution
