Statement I ∫(11+x4)dx=tan−1(x2)+C
Statement II ∫11+x2dx=tan−1x+CSolution in Punjabi
Statement I is true, Statement II is also true , Statement II is the correct explanation of Statement I.
Statement I is true, Statement II is also true, Statement II is not the correct explanation of Statement I.
Statement I is true, Statement II is false.
Statement I is false, Statement II is true .
The correct Answer is:D
Step by step video & image solution for Statement I int((1)/(1+x^(4)))dx=tan^(-1)(x^(2))+C Statement II int(1)/(1+x^(2))dx=tan^(-1)x +C by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- INDEFINITE INTEGRAL BOOK - ARIHANT MATHSCHAPTER - INDEFINITE INTEGRAL EXERCISE - Exercise (Passage Based Questions)
11 Videos
- INDEFINITE INTEGRAL BOOK - ARIHANT MATHSCHAPTER - INDEFINITE INTEGRAL EXERCISE - Exercise 5 ( Matching Type Questions )
2 Videos
- INDEFINITE INTEGRAL BOOK - ARIHANT MATHSCHAPTER - INDEFINITE INTEGRAL EXERCISE - Exercise (More Than One Correct Option Type Questions)
5 Videos
- HYPERBOLABOOK - ARIHANT MATHSCHAPTER - HYPERBOLAEXERCISE - Hyperbola Exercise 11 : Questions Asked in Previous 13 Years Exams
3 Videos
- INVERSE TRIGONOMETRIC FUNCTIONSBOOK - ARIHANT MATHSCHAPTER - INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
8 Videos
Similar Questions
If ∫f(x)cosxdx=12f2(x)+C, then f(x) can be
View SolutionFind the mean marks of the following cummulative frequency table :
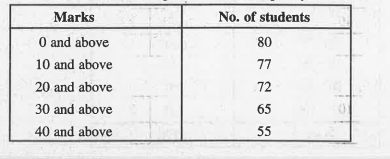

View SolutionFind: ∫dx(x+1)(x+2)
View Solutionwhich term of the following sequence : 312,3,332.....is 81?
View SolutionIf α=3sin−1(611andβ=3cos−1(49), where the inverse trigonometric functions take only the principal values, then the correct options (s) is (are)
View Solution∫dxx2+2x+2equals(A) xtan−1(x+1)+C (B) tan−1(x+1)+C(C) (x+1)tan−1x+C (D) tan−1x+C
View Solutionif ∫11+sinxdx=tan(x2+a)+C then
View SolutionEvaluate:
(i) ∫(tanx+cotx)2 dx
(ii) ∫1−cos2x1+cos2x dx
View Solutionint(1)/(1+3cos^(2)x)dx=(1)/(2)tan^(-1)((tan x)/(2))+c
View Solution(i)∫tan−1(1+x2)dx (ii)∫1√1−x2sin−1xdx
View Solution(i)∫1(1+x2)tan−1xdx (ii)∫etan−1x1+x2dx
View SolutionStatement I ∫(11+x4)dx=tan−1(x2)+C
Statement II ∫11+x2dx=tan−1x+C
View SolutionStatement I ∫2tan−1xd(cot−1x)=2tan−1xln2+C
Statement II ddx(ax+C)=axlna
View Solution{:(,"स्तम्भ (A)",,"स्तम्भ(B)"),(1.,intcot x dx ,a.,(1)/(2) log x +c),(2.,int tan x dx,b.,(1)/(2)tan x +c ),(3.,int(dx)/(1+cos2x),c.,log ( sinx ) +c ),(4.,int ( 1+ tan^(2)x)dx ,d.,log(secx ) + c ),(5.,int cosec x dx ,e.,tan x + c ),(,,f.,log ( tan .(x)/(2))+c ):}
View Solution(i) ∫dx√a2−x2=1asin−1(xa)+c
(ii) ∫dxa2+x2=tan−1(xa)+c
(iii) ∫x+1x2+2x+1dx=12log∣∣(x2+2x+1)∣∣
(iv) ∫dxx(x−1)dx=log∣∣∣x−1x∣∣∣+c
State which pair of the statement given above is true.
View Solution(i) ∫sin(tan−1x)1+x2dx
(ii) ∫sin(2tan−1x)1+x2dx
View Solution
