Let f:R→R be a function as f(x)=(x-1)(x+2)(x-3)(x-6)-100. If g(x) is a polynomial of degree ≤3 such that ∫ g(x) f(x) dx does not contain any logarithm function and g(-2)=10. ThenSolution in Punjabi
-136
-100
-84
-68
The correct Answer is:C
Step by step video & image solution for Let f:R→R be a function as f(x)=(x-1)(x+2)(x-3)(x-6)-100. If g(x) is a polynomial of degree ≤3 such that ∫ g(x) f(x) dx does not contain any logarithm function and g(-2)=10. Then by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- INDEFINITE INTEGRAL BOOK - ARIHANT MATHSCHAPTER - INDEFINITE INTEGRAL EXERCISE - Exercise 5 ( Matching Type Questions )
2 Videos
- INDEFINITE INTEGRAL BOOK - ARIHANT MATHSCHAPTER - INDEFINITE INTEGRAL EXERCISE - Exercise (Single Integer Answer Type Questions)
9 Videos
- INDEFINITE INTEGRAL BOOK - ARIHANT MATHSCHAPTER - INDEFINITE INTEGRAL EXERCISE - Exercise (Statement I And Ii Type Questions)
5 Videos
- HYPERBOLABOOK - ARIHANT MATHSCHAPTER - HYPERBOLAEXERCISE - Hyperbola Exercise 11 : Questions Asked in Previous 13 Years Exams
3 Videos
- INVERSE TRIGONOMETRIC FUNCTIONSBOOK - ARIHANT MATHSCHAPTER - INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
8 Videos
Similar Questions
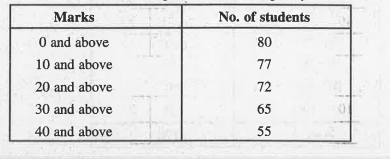
Find the mean marks of the following cummulative frequency table :

View SolutionIf ∫(2x+3)dxx(x+1)(x+2)(x+3)+1=C−1f(x) where f(x) is of the form of ax2+bx+c, then(a+b+c) equals to …….
View SolutionSolve dydx+yx=logx.
View Solutionwhich term of the following sequence : 312,3,332.....is 81?
View SolutionIf α=3sin−1(611andβ=3cos−1(49), where the inverse trigonometric functions take only the principal values, then the correct options (s) is (are)
View SolutionLet f:R→R be any function. Defining g:R→R by g(x)=|f(x)| for x→R. Then g, is
View SolutionLet f:R→R and h:R→R be differentiable functions such that f(x)=x3+3x+2,g(f(x))=xandh(g(g(x)))=x for all x∈R. Then, h'(1) equals.
View SolutionLet f:R→R be a function as
f(x)=(x−1)(x+2)(x−3)(x−6)−100. If g(x) is a polynomial of degree ≤3 such that ∫g(x)f(x)dx does not contain any logarithm function and g(−2)=10. Then
The equation f(x)=0 has
View SolutionLet f:R→R be a function as
f(x)=(x−1)(x+2)(x−3)(x−6)−100. If g(x) is a polynomial of degree ≤3 such that ∫g(x)f(x)dx does not contain any logarithm function and g(−2)=10. Then
The minimum value of f(x) is
View SolutionLet f:R→R be a function as
f(x)=(x−1)(x+2)(x−3)(x−6)−100. If g(x) is a polynomial of degree ≤3 such that ∫g(x)f(x)dx does not contain any logarithm function and g(−2)=10. Then
∫g(x)f(x)dx, equals
View SolutionLet f(x)=x3+3x+2 and g(x) is inverse function of f(x) then the value of g'(6) is
View SolutionLet the function f:R→R be defined byf(x)=x3−x2+(x−1)sinxandletg:R→R be an arbitrary function Let fg:R→R be the function defined by (fg)(x)=f(x)g(x). Then which of the folloiwng statements is/are TRUE ?
View SolutionIf ∫dxx2+ax+1=f(g(x))+c, then f(x) is inverse trigonometric function for |a|>2 f(x) is logarithmic function for |a|<2 g(x) is quadratic function for |a|>2 g(x) is rational function for |a|<2
View SolutionLet f:R→R and h:R→R be differentiable functions such that f(x)=x3+3x+2,g(f(x))=xandh(g(g(x)))=x for all x∈R. Then, h'(1) equals.
View SolutionIf f(x)=2x+3andg(x)=9x+6, then find g[f(x)]−f[g(x)]
View SolutionLet f:R→R and h:R→R be differentiable functions such that f(x)=x3+3x+2,g(f(x))=xandh(g(x))=x for all x∈R. Then, h'(1) equals.
View Solution
