Jerry had some chocolates and candies. The number of chocolates was 2 more than twice the number of candies. The candies were x in number.
The total number of chocolates with Jerry equals
2x - 2
x + 2
2x + 2
x - 2
To find the total number of chocolates Jerry has, we can follow these steps:
1. Identify the number of candies:
Let the number of candies be represented by x.
2. Calculate twice the number of candies:
The problem states that the number of chocolates is 2 more than twice the number of candies. To find twice the number of candies, we multiply x by 2:
Twice the number of candies=2×x=2x
3. Add 2 to twice the number of candies:
Since the number of chocolates is 2 more than twice the number of candies, we add 2 to the result from the previous step:
Number of chocolates=2x+2
4. Final expression for the total number of chocolates:
Therefore, the total number of chocolates Jerry has is:
Total number of chocolates=2x+2
Summary:
The total number of chocolates with Jerry equals 2x+2.
Let the number of candies be represented by x.
The problem states that the number of chocolates is 2 more than twice the number of candies. To find twice the number of candies, we multiply x by 2:
Twice the number of candies=2×x=2x
Since the number of chocolates is 2 more than twice the number of candies, we add 2 to the result from the previous step:
Number of chocolates=2x+2
Therefore, the total number of chocolates Jerry has is:
Total number of chocolates=2x+2
The total number of chocolates with Jerry equals 2x+2.
Topper's Solved these Questions
Similar Questions
There are some chocolates with Tom and Jerry. If Tom gives certain number of chocolates to Jerry, then the number of chocolates with them will be interchanged. Instead, if Jerry gives same number of chocolates to Tom, then the number of chocolates with jerry will be one-fourth of the number of chocolates that Tom has. If the total number of chocolates with them is 100, then find the number of chocolates with Tom
View SolutionThe number of books in Andy's bag equals x. If Sam has 3 more books than twice the number of books with Andy, then the number of books with Sam equals
View Solution
Knowledge Check
In a group of goats and hens, the total number of legs is 12 more than twice the total number of heads. The number of goats is
A8B6C2DCannot be dterminedAjay and Vijay have 25 chocolates in total. If Ajay gives 3 chocolates to Vijay, then the number of chocolates with them is in ratio 2:3. Find the number of chocolates with Ajay and Vijay respectively.
A20,30B15, 10C10, 15DNone of theseAjay and Vijay have 25 chocolates in total. If Ajay gives 3 chocolates to Vijay, then the number of chocolates with them is in ratio 2:3. Find the number of chocolates with Ajay and Vijay respectively.
A20,30B15,10C10,15DNone of these
Three persons, A, B and C, have a certainvnumber of chocolates with each of them.The number of chocolates with B is 20% more than that with A, which, in turn, is two-thirds of that with C. If the numberof chocolates with B is less than thetotal number of chocolates with A and C together by x percent, what is the value of x?
View SolutionThere are two boxes, red and white in colour. The ratio of the number of chocolates in the white box to the number of biscuits in the red box is 3:2 and the ratio of the number of biscuits in the white box to the number of chocolates in the red box is 3:4. If the ratio of the total number of chocolates and biscuits in the white box to the total number of chocolates and biscuits in the red box is 15:16. Find the ratio of the total number of chocolates to the total number of biscuits in the two boxes.
View SolutionJoshna and Vijay have some chocolates, The num-ber of chocolates with Joshna is two -third of the number of chocolates with Vijay. If Vijay gives five chocolates to Joshna, then both will have equal number of chocolates. How many chocolates does Joshna have ?
View SolutionTwo friends Phil and Steve participated in a chocolate eating competition. Phil ate five chocolates less than thrice the number of chocolates eatenj by Steve. If Steve ate C chocolates, then which of the following expressions is equivalent to the number of chocolates eaten by Phil?
View SolutionThe following table shows the number of chocolates four friends have.
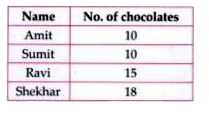
Two friends share the same number of chocolates. The number of chocolates each of them has, is ________ .
View Solution
