Ther are two biludings P and Q. If 15 persons are sent from P to Q, then the number of per sons in each biluding is the same. If 20 persons are sent from Q to P, then the number of persons in P is double the number of persons in Q. How many persons are there in building P?
80
140
120
90
The correct Answer is:C
Let's solve the problem step by step.
Step 1: Define Variables
Let the number of persons in building P be P and the number of persons in building Q be Q.
Hint: Start by defining the variables for the unknowns in the problem.
Step 2: Set Up the First Equation
According to the problem, if 15 persons are sent from P to Q, then the number of persons in each building becomes equal. This can be expressed as:
P−15=Q+15
Rearranging this gives:
P=Q+30(Equation 1)
Hint: Use the information about the equal number of persons after transferring to form your first equation.
Step 3: Set Up the Second Equation
Next, if 20 persons are sent from Q to P, then the number of persons in P becomes double the number of persons in Q. This can be expressed as:
P+20=2(Q−20)
Expanding this gives:
P+20=2Q−40
Rearranging this gives:
P−2Q=−60(Equation 2)
Hint: Use the second scenario to create another equation that relates P and Q.
Step 4: Substitute Equation 1 into Equation 2
Now, substitute P from Equation 1 into Equation 2:
(Q+30)−2Q=−60
This simplifies to:
30−Q=−60
Rearranging gives:
Q=90
Hint: Substitute the expression for one variable into the other equation to find the value of one variable.
Step 5: Find the Value of P
Now that we have Q, substitute it back into Equation 1 to find P:
P=Q+30=90+30=120
Hint: Use the value of the variable you just found to calculate the other variable.
Conclusion
The number of persons in building P is 120.
Final Answer: There are 120 persons in building P.
Let the number of persons in building P be P and the number of persons in building Q be Q.
According to the problem, if 15 persons are sent from P to Q, then the number of persons in each building becomes equal. This can be expressed as:
P−15=Q+15
Rearranging this gives:
P=Q+30(Equation 1)
Next, if 20 persons are sent from Q to P, then the number of persons in P becomes double the number of persons in Q. This can be expressed as:
P+20=2(Q−20)
Expanding this gives:
P+20=2Q−40
Rearranging this gives:
P−2Q=−60(Equation 2)
Now, substitute P from Equation 1 into Equation 2:
(Q+30)−2Q=−60
This simplifies to:
30−Q=−60
Rearranging gives:
Q=90
Now that we have Q, substitute it back into Equation 1 to find P:
P=Q+30=90+30=120
The number of persons in building P is 120.
Topper's Solved these Questions
Similar Questions
Direction: Study the given information carefully and answer the following questions. Eight people P, Q, R, S, T, U, V and W buy different items but not necessarily in the same order. Two people buy items between P and S. One person buys between T and Q. T buys an item before Q. At least two people buy after Q. Three people buy items between V and Q. V neither buy at first nor at last. The number of persons buy items before T is same as the number of persons buy the item after W. Two people buy item between W and P. R buys before U.
The number of persons buy item before S is same as the number of persons buy item after ____?
View SolutionDirection: Study the given information carefully and answer the following questions. Eight people P, Q, R, S, T, U, V and W buy different items but not necessarily in the same order. Two people buy items between P and S. One person buys between T and Q. T buys an item before Q. At least two people buy after Q. Three people buy items between V and Q. V neither buy at first nor at last. The number of persons buy items before T is same as the number of persons buy the item after W. Two people buy item between W and P. R buys before U.
How many persons buy the item after U?
View Solution
Knowledge Check
There are two examination halls P and Q. If 10 students shifted P to Q, then the number of students will be equal in both the examination halls. If 20 students shifted from Q to P,then the students of P would be doubled to the students of Q. The numbers of students would be in P and Q, respectively are
A60, 40B70, 50C80, 60D100, 80The distance between points P and Q is 485 km. If a person starts from point P with the speed of 60 km/h and another person is running with a certain speed from point Q and they both meet after 2.5 hours then find the speed of the person who starts from point Q
A140 km/hB126 km/hC156 km/hD134 km/hIf the number p is 5 more than q and the sum of the squares of p and q is 55, then the product of p and q is
A10B-10C15D-15
Direction: Study the given information carefully and answer the following questions. Eight people P, Q, R, S, T, U, V and W buy different items but not necessarily in the same order. Two people buy items between P and S. One person buys between T and Q. T buys an item before Q. At least two people buy after Q. Three people buy items between V and Q. V neither buy at first nor at last. The number of persons buy items before T is same as the number of persons buy the item after W. Two people buy item between W and P. R buys before U.
How many persons buy item between R and W?
View SolutionThree persons P, Q and R are standing in a queue. There are eight persons between P and Q and twelve persons between Q and R. If there be seven are persons ahead of R and twenty-eight persons behind P, what could be the minimum number of persons in the queue?
1) Data inadequate
2) 58
3) 40
4) 42
5) None of these
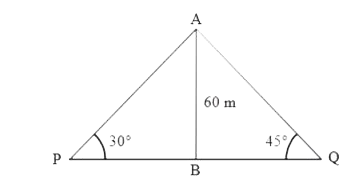
View SolutionIn the figure, two persons are standing at the opposite direction P & Q of the tower. If the height of the tower is 60 m then find the distance between the two persons.
View SolutionIf the number p is 5 more than q and the sum of the squares of p and q is 55, then the product of p and q is
View SolutionA, Q, Y, Z are different persons. Z is the father of Q . A is the daughter of y and y is the son of Z. If P is the son of Y and B is the brother of P, then
View Solution
